An Analysis of the Gyroball
This article was written by Dave Baldwin - Alan Nathan
This article was published in 2007 Baseball Research Journal
Baseball has been around for over 150 years, and during that time many thousands of pitchers, hoping to find the unhittable pitch, have experimented with grip, delivery, and release of the ball. Consequently, rarely is there anything new under the sun in the modern game. When a potentially new pitch comes along, therefore, it can generate a great deal of uncritical excitement and media attention. Such was the case with a recent, highly touted “innovation” called the “gyroball.”
The gyroball was the brainchild of Kazushi Tezuka, a Japanese pitching coach, and Ryutaro Himeno, a Japanese computer scientist who determined the properties of the pitch through elaborate simulations. Their book (in Japanese only), Makyuu no Shoutai (Roughly translated as The Secret of the Demon Miracle Pitch), published in 2001, first described the spin and behavior of the gyroball, as well as the mechanics used in delivering the pitch.1
The gyroball story seemed to grow as information was translated from Japanese to English. During 2006 articles extolling the near-magical qualities of the gyroball appeared in many publications and on many websites (see Bibliography for examples), although these properties were not claimed by Tezuka and Himeno. An article in Esquire magazine described the so-called demon pitch as “the first entirely new baseball pitch to emerge since the split-fingered fastball in the 1970s.”2
In the United States, the gyroball became a media goldmine when word spread that Daisuke Matsuzaka, an outstanding Japanese pitcher, threw this pitch— maybe—or at least was considering throwing it. As Matsuzaka negotiated a contract with the Boston Red Sox, the gyroball became one of baseball’s hottest topics.
In this paper, we describe and evaluate the physics and psychology of the gyroball. Along the way, we will point out some of the many unwarranted assumptions and claims that have been made for this pitch.
THE MECHANICS OF THE GYROBALL
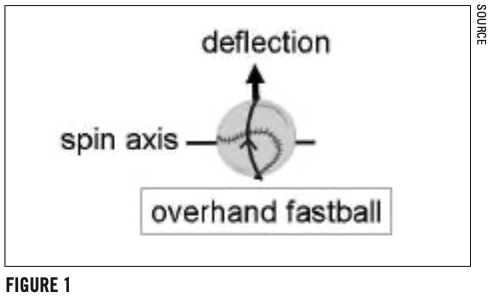
The trajectory of a pitch in flight is governed by the gravitational force, drag force, and the Magnus force on a spinning ball. Gravity makes the ball drop by three to four feet—the slower the pitch, the longer gravity acts and the greater the drop. The drag force results from air resistance to the movement of the ball. It acts to slow the pitch. The Magnus force deflects the ball, the direction and magnitude of the deflection depending on the spin rate, the speed of the pitch, and the orientation of the spin axis. This force causes the ball to break in the direction that the leading hemisphere (face) of the ball is turning. The Magnus force is largest when the spin axis and trajectory are at 90° to each other and is exactly zero when they are perfectly aligned.
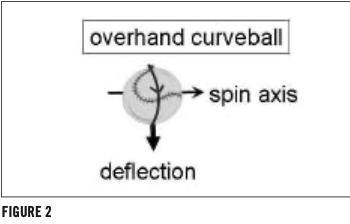
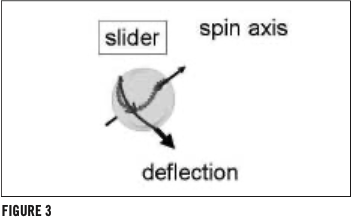
On all conventional pitches (except a perfectly non-spinning knuckleball) the spin passes over some portion of the ball’s face. For example, the backspin of an overhand fastball has a spin axis that is perpendicular to the pitch’s trajectory. This 90° axis angle produces the maximum lift, a force that partially counteracts the gravitational force (Figure 1). Therefore, with strong lift and a short flight time, the fastball won’t drop nearly as much as an overhand curveball, which is slower and has a downward Magnus force (Figure 2). The slider has a diagonal spin over the face; consequently, the pitch has a side break component and a downward break component (Figure 3).
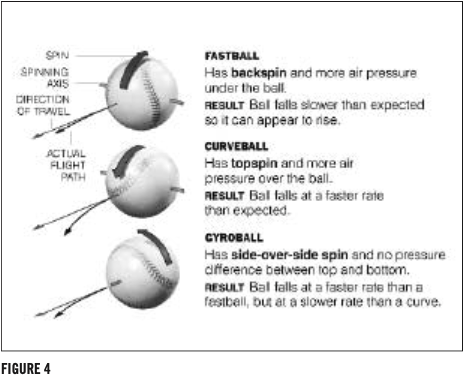
The defining feature of the gyroball is the unusual angle of the ball’s spin axis. The gyroball’s spin axis is collinear with the trajectory of the pitch; thus, the spin is perpendicular to the ball’s path. The face of the ball is spinning around a spin axis pole, which is located in the center of the face. The spin of the gyroball does not pass over any portion of the ball’s face. Since the Magnus force depends on the angle between the spin axis and the trajectory, and this angle is zero in the gyroball, the net Magnus force on the ball is zero. The only forces acting on the gyroball are gravity and drag. Figure 4 compares the spin and behavior of the fastball, curveball, and gyroball, as illustrated in a New York Times article.3
As there is no Magnus force acting on the gyroball, the exaggerated break reported in a number of publications is false. Esquire contributed to the unsubstantiated claims by saying the pitch “breaks as much as three feet before entering the strike zone.” On CBS News sportswriter Will Carroll says, “It takes a hard left turn.”4 The Seattle Post-Intelligencer reported, “To the right-handed batter the ball appears to be coming right at them like a hanging curveball, then takes a drastic dive across the plate.” The article mentions, however, that the gyroball “could be baseball’s next big pitch. Or it could be a myth.”5 Popular Mechanics described Himeno’s simulated gyroball: “whirling clockwise as it flew forward, the virtual ball curved as abruptly as its closest relative, the slider, but without sinking.” This article, too, admitted the pitch could be “a complete and total sham.”6
The gyroball requires a delivery that is different from that of other pitches. The pitcher must create the desired spin axis by establishing the ball’s equator with appropriate finger pressure upon release. As Tezuka describes the delivery, the arm angle is low— no higher than sidearm. Those few pitchers who are reported to be throwing the pitch in Japan are all sidearmers or submariners. Unlike the supine hand orientation used on the delivery of a curve, though, the hand is pronated as the ball is released. The ball rolls off the thumb side of the tips of the index and second fingers. The thumb is pointing downward on the follow-through. The pronation of the hand is claimed to be unlikely to damage the pitcher’s elbow.
WHY WOULD THE GYROBALL BE EFFECTIVE?
The gyroball might fool the hitter in at least four ways. First, the gyroball has no Magnus force to lift it against gravity (as does a fastball) or to augment the pull of gravity (as does a curveball). The batter who is looking for a fastball will see a pitch that drops about fifteen inches more than the fastball would. The batter will tend to swing too high on such a pitch. The gyroball drops much less than a curveball, so if the batter is looking for a curve, he will swing under the pitch.
Second, the release of the gyroball directs much of the force of the fingers into creating the unusual spin rather than imparting forward velocity to the pitch. As this reduces the forward velocity without slowing the arm’s motion, the gyroball can be effective as a changeup. The unexpected slower speed of the gyroball will cause the batter to underestimate the drop and overestimate the final height of the pitch. As a result, the batter will tend to swing too high.
Third, ballplayers are accustomed to seeing the spin coming across some part of the face of a ball in flight. This is the case for any ball, thrown or batted, that the player catches, and it is the case for any pitch the player tries to hit (except the gyroball). Seeing that aspect of the gyroball might be an experience unusual enough to confuse the batter. Perhaps the batter needs new skills to judge the speed of a ball that is spinning perpendicular to the trajectory.
Fourth, the batter who is looking for a slider might mistake the appearance of the gyroball’s face for that of the slider. A slider thrown off a four-seam fastball grip displays a red dot (at the location of the axis pole) in the upper right quadrant of the face (from a right-handed pitcher—upper left quadrant from a lefty).7 The dot appears in the center of the face on the gyroball, but this is close enough to the slider’s dot that a batter might find it difficult distinguishing between the pitches. The gyroball could be an effective pitch against a batter who has been set up for it with a slider.
Occasionally, some pitchers accidentally tilt the axis of an intended slider so that the axis pole is centered in the face. This pitch is called a backup slider because the catcher, anticipating that the pitch will break, must “back up” his glove in order to catch it. It can confuse both catcher and batter, but it isn’t thrown deliberately, so batters can’t be set up for it. The backup slider has the same spin characteristics as a gyroball.
DOES DAISUKE MATSUZAKA THROW A GYROBALL?
Does he or doesn’t he? This question was discussed at great length in the media in the early weeks of the 2007 season. Matsuzaka himself has been rather coy about it. When asked whether he throws the gyroball he replied, “I have done it in a game, but not too much. Sometimes accidentally.”8 Rather than listen to what people are saying, let’s see if we can bring science to bear on the subject.
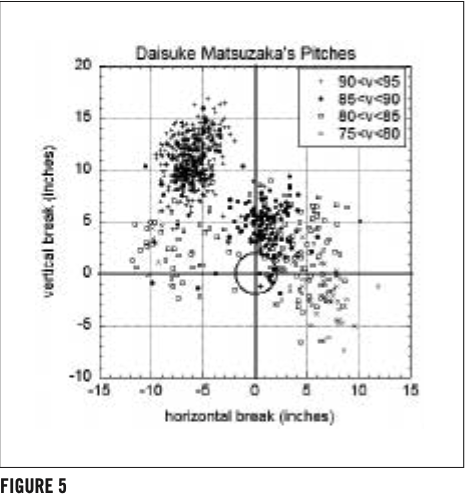
Our principal tool will be the PITCHf/x pitch-tracking system,9 which allows us to investigate in great detail each pitch thrown in every game in which the system is operating. In Figure 5 we plot each recorded pitch thrown by Matsuzaka during the first half of the 2007 season, 790 pitches in all. The figure is a scatterplot showing the vertical break versus the horizontal break, where “break” is defined to be the deviation from the trajectory due to the Magnus force. The pitches are plotted from the catcher’s view. The plot is symbol-coded by different speeds. According to our understanding of the Magnus force, a gyroball should appear near the point of zero deflection; i.e., neither a horizontal nor a vertical break is expected.
In the scatterplot we can see three distinct “clumps” of points. The pitches in the upper left cluster have speeds in the range of 90 to 95 mph. These pitches moved up and in toward a right-handed batter, as expected of a fastball thrown by a right-handed pitcher (Matsuzaka is right-handed). Therefore, this cluster represents fastballs. Directly below the fastball cluster are a number of pitches scattered above and below the zero vertical deflection line. These are probably changeups thrown off the fastball. Most of them are in the 80 to 85 mph range.
We find a second cluster of pitches a little above the zero vertical deflection line and centered to the right of the zero horizontal deflection line. Most of these pitches are in the 85 to 90 mph range. These are the characteristics we would expect of sliders. A much smaller, sparser cluster occurs below the zero vertical deflection line and with a horizontal break between four and eight inches. Here the Magnus force is augmenting gravity. The speeds of these pitches fall in the 75 to 80 mph range. These pitches are conventional curveballs, a pitch that Matsuzaka doesn’t throw often, apparently.
The gyroball has no Magnus force acting on it; therefore, there would be no vertical or horizontal break. The scatterplot shows only a few pitches close to the zero deflection point (in Figure 5 the circle illustrates a two inch radius). We conclude from this plot that very few, if any, gyroballs have been thrown by Matsuzaka in the first 790 pitches he has thrown in 2007.
SUMMARY
The gyroball is not the miracle pitch that the media has hyped it to be, but it could be an effective pitch if used with discretion. Because the gyroball’s spin is perpendicular to the pitch’s trajectory, no Magnus force would act on the ball. Therefore, the pitch will have no spin-induced deflection. Using the PITCHf/x pitch-tracking system, we examined the behavior of Daisuke Matsuzaka’s pitches to determine whether he actually threw the gyroball during the first half of the 2007 season. We conclude he likely did not.
Notes
-
Himeno, R. and Tezuka, K. Makyuu no Shoutai. (2001)
-
Cantor, D. “The Gyroball: Baseball’s First New Pitch in Thirty Years,” Esquire magazine, October 1, 2006. https://www.esquire.com/features/ESQ1006-ESQ100.P12-13.FINAL.REV_1
-
Jenkins, L. “Ultimate Pitch? Baseball Spin? The Japanese Gyroball Mystery,” New York Times, February 22, 2007. https://www.iht.com/articles/2007/02/22/sports/gyroball.php
-
CBS News story, “Don’t Call It a Curveball,” October 22, 2006. http://tinyurl.com/y5pomj
-
Andriesen, D. “The Gyroball: Miracle or Myth?” Seattle Post-Intelligencer, October 18, 2006. http://seattlepi.nwsource.com/baseball/289073_gyroball18.html
-
Coburn, D. “Tech Watch: Pitch Perfect,” Popular Mechanics, November 2006. https://www.popularmechanics.com/outdoors/sports/4199557.html
-
Baldwin, D., Bahill, T., Nathan, A. “Nickel and Dime Pitches,” Baseball Research Journal #35, SABR, 2006, 25-29.
-
Passan, J. “Searching for Baseball’s Bigfoot,” Yahoo! Sports, March 13, 2006. http://sports.yahoo.com/mlb/news?slug=jp-gyro031306&prov=yhoo&type=lgns
-
http://webusers.npl.uiuc.edu/~a-nathan/pob/pitchtracker.html