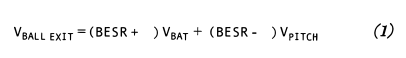Ball Exit Speed Ratio (BSER)

The NCAA requires that all nonwood bats be certified so as to limit their “liveliness.” The certification process is accomplished by measuring the performance of a bat under controlled conditions and then assigning a number to it; this number is known as the BESR (Ball Exit Speed Ratio). To be certified, the BESR of the bat must fall at or below a predetermined value set by the NCAA. This paper discusses the concept of the BESR.

The Ball-Bat Collision

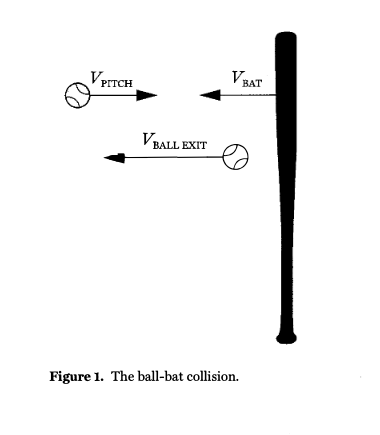
Figure 1 shows a ball and a bat just before the collision and the ball just after the collision (the position of the ball after the collision has been moved downward for the sake of clarity). The speeds involved in the collision are:

What is the BESR?

The BESR is a number, once known, that allows one to determine the ball exit speed VRALL EXIT when the bat speed VBAT and the pitch speed VPITCH are specified. The relationship between the BESR and these speeds is:

As an example, suppose the BESR for a particular ball-bat collision is 0.65, and the bat and pitch speeds are VBAT = 70 mph and VPITCH = 75 mph. The ball exit speed would be

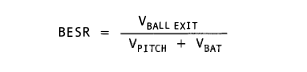
Conversely, if one measures the bat speed, the pitch speed, and the ball exit speed, then Equation 1 can be used to determine the BESR (see Equation 2 below). 

Note from Equation 1 that greater values of the BESR give rise to greater ball exit speeds. Therefore, the BESR is a measure of the “liveliness” of the ball-bat collision and it includes, for example, any “trampoline” effect that the non-wood bat may display (due to its barrel being temporarily deformed by the ball during the collision).

Where Does BESR Get its Name?

When one algebraically solves Equation 1 for the BESR the result is

When the speeds of the pitched ball and bat are the same (VPITCH=VBAT), Equation 2 becomes

We see in this case that the BESR is equal to the ratio of the ball exit speed VBALL EXIT to the relative speed (VPITCH + VBAT) of the pitched ball and bat before the collision. Hence, the name “Ball Exit Speed Ratio.”

HOW BESR DEPENDS ON THE PROPERTIES OF THE BALL AND BAT

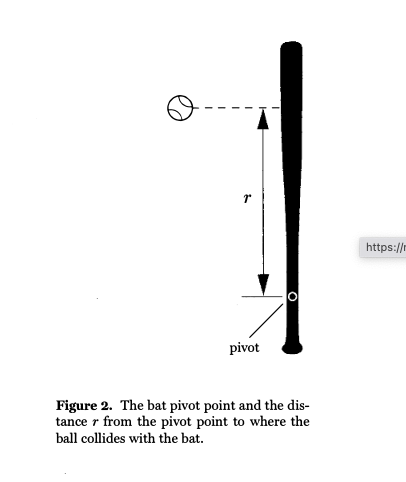
Figure 2 illustrates a ball just before colliding with the bat. The bat is assumed to be clamped in a hitting machine and is free to rotate in the plane of the paper about the pivot point.

The physics of the collision is described by applying the law of conservation of angular momentum to the ball-bat interaction. When this law is used, along with the definition of the coefficient of restitution (see below), we arrive at Equation 1, where the BESR is given in terms of the properties of the ball and bat[1][2][3]:

Note that BESR depends on the properties of the ball (m), the bat (Ip), and the ball-bat collision (e and r).

WHY USE THE BESR RATHER THAN SPECIFY A BALL EXIT SPEED?

In general, different bat testing laboratories use different types of hitting machines: (1) the pitched ball is moving and the bat is initially stationary, (2) the ball is stationary and the bat is initially moving, and (3) both the pitched ball and bat are initially moving. Even if each type of hitting machine is set up to have the same relative speed (VPrrcH + VBAT) of the pitched ball and bat, the ball exit speeds will be different. However, all types of machines. will give the same value for the BESR. This result, while not obvious, is a direct consequence of Equation 1.

WHAT IS THE MAXIMUM ALLOWED VALUE FOR THE BESR?

When bats were first tested in 1999, an initial lot of baseballs was used. The tests were conducted by using a pitch speed of 70 mph and a bat speed (at a point 6 inches from the end of the barrel) of 66 mph. Under these conditions, the best major league wood bat yielded a BESR of 0.728, which the NCAA then set to be the maximum allowed value.

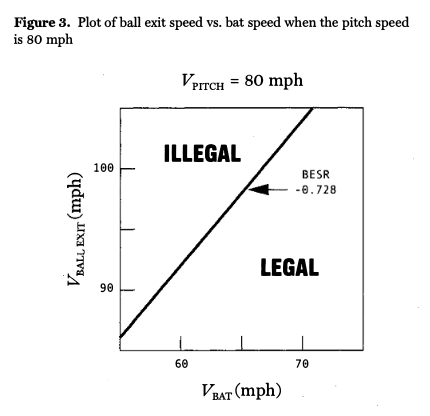
Figure 3 shows a plot of ball exit speed (VBALL EXIT) versus bat speed (VBAT) for the case when the pitch speed is VPrrcH = 80 mph. The straight line represents Equation I in which the BESR has been set to the legal limit of 0.728. Any bat that gives rise to a ball exit speed at or below this line is legal. Likewise, any bat that produces a ball exit speed above this line is illegal. 

Subsequent tests on non-wood bats used different lots of new baseballs. Because the properties of balls differ from lot to lot, even when they are stored and used in a humidity-controlled room, the BESR is adjusted to account for these differences. Therefore, the maximum allowed value for the BESR changes slightly, depending on the particular lot of baseballs used in testing a given non-wood bat. However, in every case, the BESR of the non-wood bat is always compared with that of major league wood bats tested in the same machine with the same lot of baseballs under standardized ball-bat testing conditions.

DR. KENNETH JOHNSON is a Professor of Physics, Emeritus at Southern Illinois University. DR. JAMES ASHTON-MILLER is a Research Professor in the Departments of Mechanical Engineering and Biomedical Engineering at the University of Michigan. He is a past president of the American Society of Biomechanics. DR. MICHAEL CARROLL is former Dean of the George Brown School of Engineering at Rice University. DR. ALAN NATHAN has been a professor of physics at the University of Illinois since 1977, with a specialty in experimental nuclear/particle physics. These four professors comprise the NCAA Baseball Research Panel.

 

Notes

1. Carroll, M. M. “Assessment and regulation of baseball bat performance,” Symposium on Trends in the Application of Mathematics to Mechanics, edited by P.E. O’Donoghue and J. N. Flavin (Elsevier, Amsterdam, 2000), p. 17.

2. Nathan, A. M. “Dynamics of the baseball-bat collision;” Am. J. Phys. 68, 979-990 (2000).

3. Nathan, A. M. “Characterizing the performance of baseball bats,” Am. J. Phys. 71 (2), 134-143 (February 2003).