Breaking Balls with a Runner on Third: A Game Theoretical Analysis of Optimal Behavior

With a runner on third base, the pitcher faces a dilemma. Throwing breaking balls is risky because the ball may go past the catcher, thereby allowing the runner to score without a hit. But if the pitcher avoids throwing breaking balls altogether, the batter can anticipate fastballs exclusively, increasing his ability to record a hit, which scores the runner anyway. Using a game theoretical framework, this article shows how each player optimally solves the dilemma.

INTRODUCTION

With a runner on third base, the pitcher faces a dilemma. Throwing breaking balls is risky because the ball may go past the catcher, thereby allowing the runner to score without a hit. But if the pitcher avoids throwing breaking balls altogether, the batter can anticipate fastballs exclusively, increasing his ability to record a hit, which scores the runner anyway.

Using a game theoretical framework, this article shows how each player optimally solves the dilemma. Our intuition (and the broadcasters we listen to) might tell us that, to decrease the likelihood of the runner scoring on a wild pitch or passed ball, the pitcher increases his fastball frequency. Consequently, the batter anticipates more fastballs and is therefore more likely to record a hit, as the pitcher has adopted a more predictable strategy.

In actuality, after solving each player’s optimal strategy, it turns out only one part of this intuition is correct. When the players strategize correctly, the batter anticipates more fastballs. However, the pitcher continues throwing breaking balls at the same frequency as before, which makes the batter equally successful at guessing the correct pitch with a man on third base as with third base empty.

THE MODEL

To establish a baseline for comparison, I begin this section by formally defining a pitching situation with the bases empty. I then introduce the added tradeoff of a man on third and find the solution of the more complex game. Afterward, I compare the results of the two models to prove my claims.

With the Bases Empty. For ease of analysis, I consider a model where the pitcher has only two pitches: fastball and slider. Although most pitchers throw more than two types, the results presented below straightforwardly extend to cases where the pitcher has more than two pitches.

To capture the batter’s advantage from correctly guessing the type of pitch thrown to him, I begin by considering a simple, simultaneous move game. The batter has two actions: guess fastball and guess slider. The pitcher has two actions: throw fastball and throw slider. If the batter guesses correctly, he earns 1 point and the pitcher earns -1. If the batter guesses incorrectly, both players earn 0.

The preference ordering models the batter’s ability to hit a fastball equal to his ability to hit a slider. In practice, this is not the case, but the results presented here extend to cases where the batter has a strong pitch and a weak pitch. The important feature of these payoffs is that they exclude trivial cases where the batter cannot hit a particular pitch at all or the pitcher cannot adequately throw a particular pitch.

I make this assumption to create a more parsimonious model. Relaxing the assumption does not change the results but does make the corresponding analysis far less intuitive. Specifically, we could alter the payoffs to read as the probability each player’s team wins the game given the players’ strategy selections. In this manner, we could fully account for a pitcher throwing sliders blocked in the dirt that the batter cannot hit, or a batter’s particular weakness to a fastball or slider. However, the results presented still hold in this generalized case.

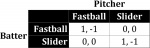Figure 1 is the payoff matrix that represents each player’s strategies and preferences. By convention, the row player’s payoff is the left numbers in each cell while the column player’s payoffs is the right number.

Since this is a simultaneous move game of complete information, I solve for its Nash equilibria. A Nash equilibrium is a set of strategies such that, given what the other player is doing, no player has incentive to change his strategy. In other words, no player can play a different strategy and improve his expected outcome.

It is easy to see that there are no Nash equilibria in pure strategies, or single strategies players use exclusively. For example, suppose the pitcher always threw a fastball. Then the batter’s best response is to always guess fastball. But if the batter is always guessing fastball, then the pitcher ought to always throw a slider instead. However, then the batter should always guess slider. That returns us to where the pitcher always throws a fastball. The loop repeats ad nauseam.

As such, the players must randomize between their strategies; intuitively, we and the players both know that the pitcher must sometimes throw a fastball and sometimes throw a slider, while the batter must sometimes guess fastball and sometimes guess slider. The players cannot fall into a predictable pattern.

We now search for mixed strategy Nash equilibria, which cover these randomized strategies. When both players must randomize their strategies, they select probability distributions over their pure strategies that leave their opponents indifferent between the two opposing pure strategies. This will become clearer as we solve the game.

Let ?PF ? (0,1) be the probability the pitcher throws a fastball. (The pitcher therefore throws a slider with complementary probability, or 1–?PF.) Then EU_BF(?PF), the batter’s expected utility for guessing fastball, equals:

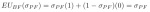
This formula is the batter’s payoff for guessing fastball multiplied by the probability the pitcher throws him a fastball plus the probability of getting a slider multiplied by the probability the pitcher throws him a slider.

Likewise, the batter’s expected utility for guessing slider equals:

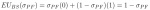
Thus, the batter is indifferent to guessing fastball and guessing slider if:

So if the pitcher throws a fastball as often as he throws a slider, the batter cannot gain an advantage by guessing one type of pitch over the other. Since he is indifferent between always guessing one type, he is also indifferent between all mixtures of guesses. That is, for ?PF=1/2, the batter’s payoff for always guessing fastball is equal to guessing fastball a quarter of the time, which is also equal to guessing fastball half the time, which is also equal to guessing fastball five-sevenths of the time, and so forth.

Next, we calculate the pitcher’s expected utility for each of his pure strategies as a function of the batter guessing fastball with probability ?BF ? (0,1).[fn]It follows that the batter guesses slider with complementary probability, or 1–?BF.[/fn] The pitcher’s expected utility of throwing a fastball equals:

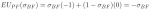
And the pitcher’s expected utility of throwing a slider equals:

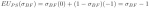
Thus, the pitcher is indifferent between throwing his two pitches if:

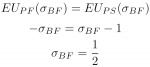
Note that when both players choose fastball and slider with equal probability, neither player can change his strategy and increase his payoff. Therefore, the game is in “equilibrium.” The intuition here is that both players need to be unpredictable.[fn]The mixtures ?BF and ?PF are equal to exactly 1/2 because the payoffs assumed the batter can hit fastballs equally as well as sliders. If we relaxed this assumption, then the mixtures would change, but how the mixtures evolve with man on third does not. In other words, making this simplifying assumption does not change the model’s substantive results.[/fn] If one begins focusing on a particular pitch, the other can exploit the situation; either the batter begins to look for that particular pitch, or the pitcher starts throwing the opposite pitch.

With a Runner on Third. We now consider a slight alteration to the previous game. To model the risk throwing a slider entails, whenever the pitcher throws a slider, the batter gains X and the pitcher loses X, where X>0.[fn]Note that when X=0, the altered game converges to the original game.[/fn] Figure 2 depicts the strategic interaction.

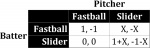To be clear, X incorporates many things: the probability the pitcher throws the ball in the dirt, the probability the catcher blocks such balls, and the speed of the runner at third. Since there is some risk that the runner scores on a wild fastball, X is the extra risk of throwing a slider.[fn]Historically, 0.24% of fastballs result in a wild pitch or passed ball, while the rate is 0.49% for changeups, 0.60% for curveballs, 0.73% for sliders, and 1.37% for knuckleballs. See “A Pitchf/x Look at Passed Palls and Wild Pitches,” Dave Allen, accessed February 24, 2012, http://baseballanalysts.com/archives/2009/11/a_pitchfx_look.php.[/fn] Both the batter and pitcher share a common evaluation for X (whether it is equal to .5, .75, 2, or whatever) before they play the game. By having X vary in this manner, we can solve for all possible scenarios and measure how the optimal strategies change as a function of the pitcher’s ability to control pitches, the catcher’s ability to block pitches, and the speed of the runner on third.

I solve for two different cases: X>1 and X?(0,1). When X=1, there is a knife-edge condition, which is substantively unrealistic.[fn]A knife-edge condition is when an input (here, X) must be equal to an exact value for the solution to hold. If we think of X as being drawn from a continuous probability distribution, then the probability of having X equal exactly 1 is 0. Consequently, the case is unrealistic and therefore unimportant.[/fn] Nevertheless, I include the proof for X=1 in the appendix.

First, suppose X>1. It is easy to see that regardless of what the batter does, the pitcher should always throw a fastball. Indeed, suppose the batter guessed fastball. Then the pitcher should throw a fastball, as -1 >-X. Now suppose the batter guessed slider. Then the pitcher should throw a fastball, as 0>-1–X. So throwing a fastball is strictly better than throwing a slider regardless of what the batter does. Thus, the pitcher always throws a fastball.

From the above reasoning, the batter can infer the pitcher will throw a fastball with certainty. Thus, he selects his best response to a fastball. He earns 0 for guessing a slider and 1 for guessing a fastball, so he guesses fastball. So when X>1, the pitcher always throws a fastball, and the batter always guesses fastball.

Second, suppose X?(0,1). As in the game with the bases empty, no pure strategy Nash equilibria exist. Despite the added X dynamic, if the pitcher always throws a particular pitch, the batter always anticipates that pitch. But if the batter always anticipates a certain pitch, the pitcher optimally throws the opposite pitch, and we devolve back to the familiar strategic loop.

Therefore, we must look for a mixed strategy Nash equilibrium using the same process as before. Again, let the probability the pitcher throws a fastball be ?PF. Then the batter’s expected utility for guessing fastball equals:

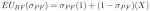
And the batter’s expected utility for guessing slider equals:

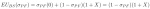
Therefore, the batter is indifferent between guessing fastball and guessing slider if:

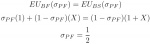
Meanwhile, let the probability the batter guesses fastball be ?BF. Then the pitcher’s expected utility of throwing a fastball equals:

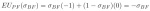
And pitcher’s expected utility of throwing a slider equals:

Thus, the pitcher is indifferent between throwing a fastball and throwing a slider if:

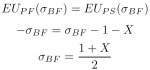
To verify that this is a valid, non-deterministic probability distribution (that is, ?BF is between 0 and 1), note that both the numerator and denominator are positive, and that 2>1+X since X?(0,1). These two properties preserve the fact that ?BF is a strictly positive number less than 1.

Therefore, in equilibrium, when X?(0,1) the pitcher throws fastballs and sliders both with probability 1/2, while the batter guesses fastball with probability (1+X)/2 and guesses slider with probability (1–X)/2.

COMPARATIVE STATICS

Comparative statics analyze changes in equilibrium behavior as a function of changes to the game’s parameters. In the strategic situation presented here, there are two such parameters: whether the bases are empty or there is a man on third, and the likelihood that a ball goes past the catcher (represented by X).

Two things are immediately apparent. First, the pitcher only changes his behavior in the case with a runner on third and X>1, where he throws fastballs exclusively. Substantively, when X>1, the pitcher is so wild, the catcher is so ineffective at blocking balls in the dirt, and the runner at third is so fast that the pitcher would rather be predictable with his fastball than risk having a slider go past the catcher.

Although mathematically possible, the situation seems unlikely at the major league level; it requires a level of pitching inconsistency and catcher incompetency unbecoming of a professional baseball player. Perhaps the only major league application is when an emergency catcher is behind the plate or a position player is on the mound. At that point, the pitcher may simply want to throw fastballs exclusively.

The second obvious difference is that the batter looks for a fastball more frequently with a runner on third and X?(0,1) than with the bases empty. To see this, recall that the probability he guesses fastball with the bases empty equals 1/2, while the probability he guesses fastball with a man on third and X?(0,1) equals (1+X)/2. Note that (1+X)/2>1/2 because X>0. So, as X increases, the probability the batter guesses fastball increases.[fn]That is, the derivative of (1 + X)/2 with respect to X equals 1/2. Since X ? (0, 1) in this case, the derivative is always positive on the relevant interval for X and thus the probability (1 + X)/2 is increasing as a function of X.[/fn]

To the observer, the batter displays a type of risk aversion here. He knows if the pitcher throws a slider, the runner will score with some probability no matter what he guessed. So guessing fastball more frequently increases his minimum payoff. However, he cannot guess fastball too often —that is, more frequently than (1+X)/2—otherwise the pitcher’s best response is to always throw a slider, despite the risk of scoring the runner from third.

Given that, the pitcher’s optimal response is sensible. Throwing sliders remains risky. Yet throwing fastballs more frequently with a runner on third plays right into the batter’s hands, as the batter could focus on fastballs exclusively. Thus, the pitcher continues to throw risky sliders, knowing that he is more likely catch the batter off guard when he does.

Another question we might be interested in is how a runner on third affects the batter’s ability to put the ball in play. To find the probability the batter is “successful” in this regard, defined as the probability that he guesses correctly, we must first calculate the likelihood of particular outcomes in each model. First, consider the game with the bases empty. The equilibrium calls for the batter to guess fastball with probability 1/2 and for the pitcher to throw a fastball with probability 1/2. The probability the batter guesses fastball and the pitch is fastball equals the probability that each such event occurs, namely (1/2)(1/2)=1/4. The probability the batter guesses slider and the pitch is slider equals (1–1/2)(1–1/2)=1/4. Therefore, the probability the batter is successful is the sum of these probabilities, or 1/4+1/4=1/2. So with the bases empty, the batter successfully guesses the correct pitch half of the time.

Now consider the game with a man on third and X>1. In equilibrium, the batter always guesses a fastball and pitcher always throws a fastball. Therefore, the batter is successful with probability 1; put differently, he always guesses correctly.[fn]The definition of success here does not imply the batter always records a hit, only that he is more likely to because he can always anticipate the pitch that is thrown to him.[/fn]

Finally, consider the game with a man on third and X?(0,1). According to the equilibrium, the batter guesses fastball with probability (1+X)/2 and the pitcher throws a fastball with probability 1/2. Therefore, the probability the batter guesses and receives a fastball equals [(1+X)/2](1/2)=(1+X)/4. Similarly, the probability the batter guess and receives a slider equals [1–(1+X)/2](1/2)=(1–X)/4. Thus, the total probability the batter is successful equals (1+X)/4+ (1–X)/4=1/2.

In comparing these results, we see that the batter only gains an advantage over the pitcher when the rate of runaway sliders is extremely high, or X>1. Outside of that, the likelihood the batter is successful equals 1/2 in both the model with the bases empty and the model with a runner on third and X?(0,1).

The pitcher’s optimal behavior explains the discrepancy between the intuition from the beginning of the article and the model’s results. Since the pitcher continues throwing fastballs and sliders at the same rate with a runner on third and Xe(0,1), the batter cannot increase or decrease the probability he records a hit; he could guess fastball or slider as a pure strategy, and he would see the same results. Therefore, to keep the pitcher honest the batter guesses fastball with increased regularity. This implies that even if a selfish batter determined to score the runner without the aid of a wild pitch or passed ball cannot strategically inflate his batting average or runs batted in focusing only on single type of pitch.

That said, the pitcher’s payoff decreases as X increases from 0 to 1. The pitcher’s expected utility is the sum of each of his payoffs times the probability that each outcome occurs in equilibrium. Recall the probability the pitcher throws a fastball equals 1/2 and the probability he throws a slider also equals 1/2. Meanwhile, the batter guesses fastball with probability (1+X)/2 and guesses slider with probability (1–X)/2. Thus, the probability the pitcher throws a fastball and the batter guesses fastball equals (1/2)[(1+X)/2], the probability the pitcher throws slider and the batter guesses fastball equals (1/2)[(1+X)/2], the probability the pitcher throws fastball and the batter guesses slider equals (1/2)[(1–X)/2], and the probability the pitcher throws a slider and the batter guesses a slider equals (1/2)[(1–X)/2]. Multiplying these probabilities by the pitcher’s payoffs in the outcomes they represent yields the pitcher’s overall expected utility:

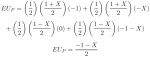
This shows that as X increases, the pitcher’s expected utility decreases.[fn]That is, the derivative of pitcher’s payoff with respect to X equals -1/2, so the payoff function is decreasing in X.[/fn] Thus, since the pitcher’s ability to control his slider and the catcher’s ability to block the slider decrease X, these skill sets increase the pitcher’s overall payoff.[fn]This result should be unsurprising. See Sean Forman, “Blocking Pitches: Assessing a Catcher’s Ability to Save Runs with Bruises” (paper presented at the 37th Annual Society for American Baseball Research convention, St. Louis, Missouri, July 26–29, 2007).[/fn] However, pitcher and catcher incompetence can only reduce the pitcher’s payoff by so much; if X>1, the pitcher always throws a fastball and the batter always guesses fastball, leading the pitcher to earn -1 with certainty.

CONCLUSION

This article investigated the strategic dynamics of pitching with a runner on third base. I found that, when players strategize optimally, a runner on third only changes the pitcher’s behavior in extreme circumstances. When the pitcher has some control over his breaking balls and the catcher can competently block balls in the dirt, pitchers optimally throw as they would with the bases empty. On the other hand, the batter focuses on fastballs, knowing that there is some chance the runner will score without a hit on a breaking ball.

Since the model provided derives specific expectations, future research could investigate whether players play according to the optimal parameters. However, this may prove complicated. Note that the model investigated a simplified world where the pitcher and batter are unconcerned about the type of out recorded. Yet, with one out, a deep fly ball out is much worse for the pitcher than a ground out, which increases the complexity of drawing direct comparisons between when the bases are empty and when there is a runner on third. Fortunately, this concern disappears with two outs, since the third out is strategically the same no matter how it is recorded.[fn]I am indebted to an anonymous reviewer for pointing out this issue and a way to work around it.[/fn] Given the incorrect intuition presented at the beginning of the article, it may very well be that players engage in suboptimal behavior.

APPENDIX

This appendix solves the game with a runner on third when X=1. To begin, note that throwing a fastball weakly dominates throwing a slider for the pitcher. Both players selecting fastball is a pure strategy Nash equilibrium. However, infinitely many partially mixed strategy Nash equilibria also exist in which the batter plays fastball as a pure strategy and the pitcher mixes.

The batter’s expected utility for guessing fastball as a function of the pitcher’s mixed strategy ?PF equals:

And his expected utility of guessing slider equals:

Therefore, the batter’s best response to ?PF is to guess fastball if:

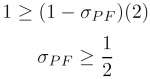
Since the pitcher is indifferent to throwing a fastball and throwing a slider when the batter is guessing fastball, any ?PF ?(1/2,1) constitutes a partially mixed strategy Nash equilibrium.

WILLIAM SPANIEL is a Ph.D. student in political science at the University of Rochester, author of the best-selling game theory textbook “Game Theory 101: The Basics,” and creator of gametheory101.com. You can contact him at williamspaniel@gmail.com.