Computers in Baseball Analysis
This article was written by George T. Wiley
This article was published in 1976 Baseball Research Journal
The most significant development in the use of statistics over the past 25 years has been with computers. Mathematical computations that formerly took hours to do by hand are completed by the computer in seconds. Masses of statistical information are now being analyzed in ways never before thought possible. In addition, when such statistical information is extensive and uniformly organized, cause-effect relationships can be determined with amazing accuracy. Baseball statistics clearly fit the definition of “extensive and uniformly organized.” The purpose of this essay is to describe what resulted when 40 years of major league team baseball statistics (1920-1959) were fed into a computer to determine the importance of certain aspects of the game- like home runs, earned run average, and stolen bases – to the final standing of the teams at the end of the season.
I. Research Procedures
In preparing the results of a research study it is customary to begin by describing both the method of collecting the information and the way the information was statistically handled. For this study these three steps were completed: (1) ranking the teams in both the American and National Leagues I through 8 on each of 17 common baseball statistics for the 40 seasons, 1920-1959; (2) processing these rankings by a computer using three mathematical operations; and (3) analyzing the computer-printed report.
Rankings. The teams were ranked for their performance in 17 categories. The 1935 National League season is an example of how this ranking was done. The total for this study was 640 teams and 10,880 units of information.
Mathematical Treatment. As is well known, a computer can calculate only what its human operator prepares it to calculate. The thousands of pieces of information described above could be processed in a countless number of ways. The second step in these research procedures was to determine what mathematical treatment should be employed to make these baseball statistics most revealing in terms of why some teams finish higher than other teams.
It was determined that correlation would be very useful. A correlation is a mathematical statement of consistency between two items that are present in similar situations. In baseball, for example, if the team that finishes first also finishes first in hitting home runs, and the team that finishes second also finishes second in home runs and so on with each team’s ranking in hitting home runs matching its final league standing, that would be a perfect correlation. Naturally, in baseball as in the rest of the real world of human activity, things rarely occur in perfect correlation. However, whenever a high correlation exists, there is ample reason to conclude that the two items change in direct relationship to one another. When this relationship is expressed in terms of home runs, earned run average, or any other key element of the game to the final standing of the teams, the value of correlation can readily be seen.
In additional to producing correlations, the computer was programmed to prepare a predictor equation, called by the mathematician a multiple regression equation. This operation analyzed all of the correlations for the 17 baseball elements examined and then determined which of them were most significant in determining the final league standing. Baseball managers and executives spend their lifetime developing such a capacity. One result of this research study is to supplement the common-sense principles like “being strong up the middle” and “dominating second-division clubs” with the results from the computer’s prediction equation.
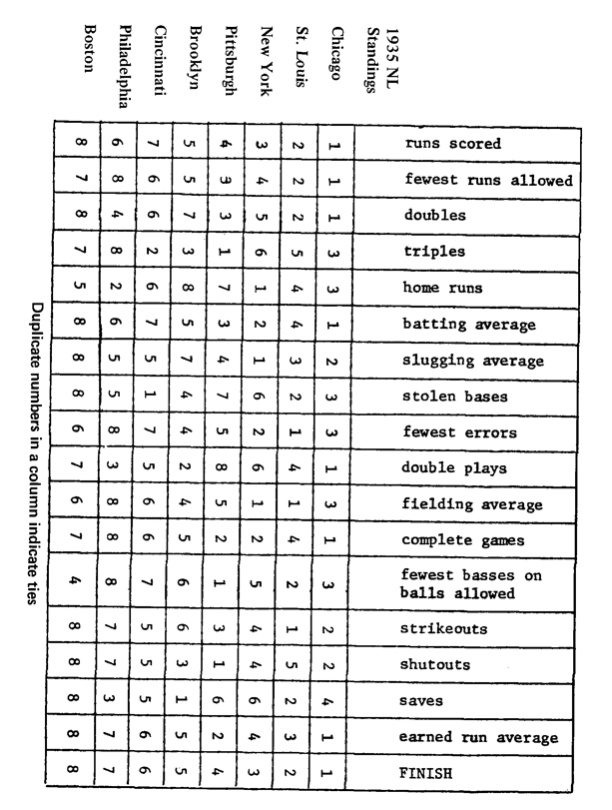
The third and final operation the computer was instructed to perform was to determine how the teams finished compared with how they should have finished based on their rankings on the 7 key aspects. Did all of the 80 sixth-place teams, for example, finish about the same in batting, pitching, and fielding; and if not, which ones finished higher or lower in the standings than their performances in the various categories warranted? The mathematical term for the above computation is a residual.
Analysis. One beauty of the computer is that it can examine baseball statistics without any predetermined bias; and, while the mathematical theories involved are almost incomprehensible to the layman, the computer results have undeniable accuracy. The final step in these procedures was to analyze the information that had been calculated and printed by the computer and prepare it in terms that the baseball researcher might appreciate.
II. Results
A high correlation, with 1.0 used to represent a perfect one, probably indicates that the two items are dependent upon one another in a cause-effect relationship. Correlations of .55 or higher are considered very significant. The five highest correlations of the 17 aspects studied with final team standing were these (the figures are correlations, not percentages):
1. fewest runs allowed .749
2. earned run average .743
3. runs scored .737
4. slugging average .642
5. batting average .615
All of these correlations are extremely high, particularly when it is recalled that the statistics of 640 teams were involved. The primary reasons why these aspects have such high correlations with final team standing can be determined by a common sense understanding of the nature of baseball. But it is significant that all of the above items are accumulative team statistics, not single aspect statistics; runs scored depend on various types of hits, plus stolen bases, opponents’ errors and the like. Fewest opponents’ runs, to use another example, depends on good pitching plus solid defense.
This point is particularly important when examining those factors of the 17 that have the lowest correlations with final team standing:
17. double plays .073
16. stolen bases .210
15. triples .298
14. doubles .343
13. fewest bases on ball allowed .368
The correlation figures for these are so low as to conclude that in themselves they have little or no effect on final team standing. In other words, the team leading the league in double plays, stolen bases, or triples is just as apt to finish in any of the eight places, while a team’s ranking on fewest runs allowed or earned run average will be just about the same as the team’s final league standing. In contrast to those items having high correlations, those with low correlation are all primarily single aspect, rather than accumulative, statistics. For example, batting average, correlating .615, is a product of all types of hits and other items determining times-at-bat, while doubles and triples are specific types of hits and stand alone as a baseball statistic. The same thing can be said for stolen bases and bases on balls. Even the double play is a specialized type of putout – flashy, but not, evidently, indispensable.
The other factors in between the highest and lowest correlations ranked as follows:
6. shutouts .547
7. most strikeouts .517
8. fielding average .498
9. fewest errors .472
10. saves .453
11. complete games .420
12. home runs .419
In addition to the above correlations with final team standing, the computer also produced information on how the various factors correlated with each other. Most of these are obvious because one of the factors is totally dependent on the other. However, it is of some value to have verification of this by the computer, because if the computer confirms what we already know to be true, then some of the other results become easier to accept. The highest eight correlations of the 17 factors with each other were:
1. fewest errors – fielding percentage .96
2. fewest runs allowed ERA .92
3. runs scored – slugging average .83
4. home runs slugging average .76
5. home runs – batting average .76
6. batting average slugging average .74
7. fewest runs allowed – shutouts .64
8. shutouts – ERA .62
Only the high correlation between home runs and batting average might cause some raised eyebrows, and reference to the years of the study, 1920-1959, might be, at best, only a partial explanation.
Of more interest, perhaps, are those items that have a very low correlation with each other. Four of these combinations actually have negative correlations. This means that the two factors do not increase or decrease together but actually when the league rank in one increases the league rank in the other decreases and vice versa.
1. double plays – most complete games -.071
2. home runs – stolen bases -.067
3. home runs – triples -.061
4. fewest bases on balls – most strikeouts -.003
None of these are significant figures mathematically, meaning there is great variance on how they might occur together in league ranking in relation to final team standing, but that there would be any negative correlations at all must be of some interest to the baseball researcher.
The other combinations fell between these extremes, with some of the more interesting being:
Batting Pitching
double – batting average .544 complete games – shutouts .365
double – home runs .198 strike outs – shutouts .357
Fielding
double plays – fielding average .139
double plays – fewest errors .103
The second mathematical treatment was the development by the computer of a predictor equation to best determine the final standing of the teams. This equation determines not only the order in which the 17 factors influence final standings but also the importance of each of the factors. One of the phenomena of this mathematical formula is that the relationship of the factors can change when they are being treated as a group from their relative importance when each in its own turn was being evaluated in terms of final team standing. As noted in the discussion above, the highest correlation with final team standing was fewest runs allowed, .749. This remains the same in the predictor equation. The second most important factor in the predictor equation is most runs scored. Together these two factors raise the prediction figure to .901, very close to the perfect figure of 1.0. The third factor, earned run average, increases the correlation to .904. In all, there are seven factors that make up the predictor equation.
- fewest runs allowed .749
plus 2. most runs scored .901
plus 3. earned run average .904
plus 4. batting average .907
plus 5. saves .910
plus 6. fielding average .912
plus 7. complete games .914
The impact of the other ten factors examined only add .003 to the effectiveness of the prediction. Actually, the first two items produce the major impact of the equation. The reason why the first two factors are the first two factors is self-evident from the nature of baseball. The significance of the remaining items, particularly why some factors are not more powerful in affecting the prediction, is a subject for additional research.
The third mathematical treatment with these 10,880 pieces of information was to compare the relationship of the actual team finish with a computerized predicted finish based on team rankings on the 17 factors. For example, the 1958 Chicago White Sox finished second, but on the basis of their performances of the 17 factors when compared to how the other 639 teams performed on the factors and where they finished, those same White Sox should have finished fourth. At the other extreme, the 1938 St. Louis Cardinals finished seventh, while the computerized prediction was 3.90. The difference between the predicted and the actual is called the residual.
One baseball discussion that often produces controversy concerns which was the best team that ever played. The residuals can be used to focus on that question. The following ten teams from 1920 to 1959 so dominated the 17 categories that they not only finished in first place but they also predicted mathematically even better than a first place finish. They had a residual that approached zero. These teams are:
Team Predicted Finish
- 1942 New York Yankees 0.16
- 1939 New York Yankees 0.32
- 1946 St. Louis Cardinals 0.33
- 1927 New York Yankees 0.45
- 1937 New York Yankees 0.50
- 1942 St. Louis Cardinals 0.52
- 1955 Brooklyn Dodgers 0.54
- 1953 New York Yankees 0.59
- 1944 St. Louis Cardinals 0.64
- 1935 Chicago Cubs 0.65
Remember, the computer treats each year equally, the determining factor being how superior a team was to its competition. This procedure does not take into account various changing conditions, like the years when quality ballplayers dominated many of the teams, the war years, the final years of the dead ball era, changes in pitching strategy, etc. Furthermore, not only did the above ten teams have to rank first or second on most of the 17 factors but also they couldn’t be very poor in any category without affecting the residual. For example, the 1927 New York Yankees would have climbed a place or two if they had not finished only tied for fifth in stolen bases and dead last in double plays. Obviously, these last two statistics don’t mean very much when fans discuss what makes a team great. For comparative purposes the Philadelphia Athletics of 1929, 1930, and 1931 predicted 1.26, 1.51 and 1.38 respectively. Also, the spread factor was not provided for by the mathematics of this study. If the #1 ranking team in home runs hit 180 and the #2 team hit 179, the weight to #2 was the same as if it had hit only 150.
At the other end of the standings, some last place teams performed so poorly on the 17 items that they mathematically predicted poorer than eighth place! The ten worst teams (1920-59) when computerized in this way were:
Team Predicted Finish
1. 1952 Pittsburgh Pirates 9.10
2. 1942 Philadelphia Phils 8.93
3. 1932 Boston Braves 8.93
4. 1954 Pittsburgh Pirates 8.83
5. 1953 Pittsburgh Pirates 8.77
6. 1951 St. Louis Browns 8.64
7. 1938 Philadelphia Phils 8.59
8. 1925 Boston Red Sox 8.55
9. 1939 Philadelphia Phils 8.54
10. 1941 Philadelphia Phils 8.53
Perhaps the most significant result from these residuals is the identification of those teams out of the 640 that were predicted by the computer to finish much lower than they actually did. Most of these did not win their respective pennants, but that fact should not diminish their accomplishment. Six of these teams finished over two places higher than predicted.
Actual Predicted
Finish Finish Difference
1958 Chicago White Sox 2 4.58 2.58
1924 Brooklyn Dodgers 2 4.19 2.19
1936 ChicagoWhite Sox 3 5.19 2.19
1943 Chicago White Sox 3 5.14 2.14
1959 Los Angeles Dodgers 1 3.13 2.13
1959 Chicago White Sox 1 3.10 2.10
On the other hand, as previously noted, one of the 640 teams, the 1938 St. Louis Cardinals, finished in seventh place, but the computer predicted them to finish better than fourth, over three places difference!
Actual Predicted
Finish Finish Difference
1938 St. Louis Cardinals 7 3.90 3.10
1952 Detroit 8 5.27 2.73
1943 Detroit 5 2.28 2.72
1954 St. Louis Cardinals 6 3.44 2.56
1923 Chicago White Sox 7 4.49 2.51
1925 New York Yankees 7 4.52 2.48
Only two teams of the 640 theoretically should have finished in first place and did not: the 1922 St. Louis Browns and the 1949 St. Louis Cardinals. Both came in second.
III. Conclusions
The primary purpose of this study was to demonstrate the use of the computer in mathematically examining baseball statistics. The specific focus was to determine the relationship of 17 individual factors to the final standing of 640 teams from 1920 to 1959.
The major conclusion reached is that pitching statistics are slightly more reliable in determining team finish than are batting statistics, and both are more significant than fielding. Composite baseball statistics like fewest runs allowed, runs scored, and earned run average are more reliable in determining finish than individual statistics like triples, most strikeouts, or double plays.
Finally, mathematical treatments and the computer should be recognized as a useful way of looking at the statistics that have been so systematically compiled throughout the history of the game. Nothing, of course, can replace the judgment and sensitivity of the baseball researcher as he approaches an analysis of the game and the men who played it. The researcher, however, should use all the means at his disposal. The computer offers the opportunity for an additional insight into baseball.


