High Altitude Offense: An Empirical Examination of the Relationship Between Runs Scored and Stadium Elevation
This article was written by Eliza Richardson
This article was published in Fall 2014 Baseball Research Journal
Although calculations have been made, computer simulations have been analyzed, and the coefficients of restitution and drag of baseballs in flight have been measured in laboratories, the actual relationship between number of home runs hit and stadium elevation has not been empirically observed over a wide range of elevations in order to compare with predicted values.1, 2, 3, 4, 5 In general the distance of the flight of a batted ball is governed by its initial launch angle and velocity. These are the two most important factors by far (and are not dependent on altitude or any other external condition). However, this simple calculation of projectile motion is complicated by additional real-world factors such as drag caused by air resistance, which decreases the distance traveled, and the Magnus force, caused by backspin-induced lift which can increase the distance traveled.
 Drag can be measured in a wind tunnel with a stationary ball, and the Magnus force can be calculated based on assumptions regarding rotation speed, but both of these kinds of studies have to rely on educated guesses because baseballs are not smooth and may rotate differently depending on the batter and the type of pitch being hit. Because the density of air decreases with increased altitude, there is less drag on an object in flight at high altitudes. This effect will increase the distance traveled by a batted ball at high altitude, as long as other atmospheric effects—wind, humidity, and temperature—are also constant.
Drag can be measured in a wind tunnel with a stationary ball, and the Magnus force can be calculated based on assumptions regarding rotation speed, but both of these kinds of studies have to rely on educated guesses because baseballs are not smooth and may rotate differently depending on the batter and the type of pitch being hit. Because the density of air decreases with increased altitude, there is less drag on an object in flight at high altitudes. This effect will increase the distance traveled by a batted ball at high altitude, as long as other atmospheric effects—wind, humidity, and temperature—are also constant.
In practice, wind has the largest effect of the three.6 Robert Adair estimates that a 10 mile per hour following wind can add 30 feet to the flight of a baseball, whereas the decreased air density between sea level and Denver alone adds only 20 feet.7 If all other factors are constant, humidity in the air is expected to increase the distance of a batted ball since water vapor is less dense than air, but balls stored in humid or cold conditions don’t travel as far because their coefficient of restitution has been compromised.8, 9 In practice, there is no simple way to characterize by simulations and calculations the competing effects of the atmosphere at different altitudes with different weather patterns and seasonal changes. In this study I use data from minor league baseball games to determine the relationship between home runs and stadium altitude.
Statistical data collected from Short Season A and Rookie League A stadiums provide a better means to determine the relationship between home runs and altitude, if one exists, than from major league stadiums for three important reasons: elevation range, roster turnover, and stadium dimensions.
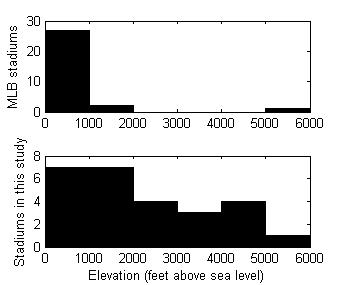
1. Elevation range. There is only one Major League Baseball stadium whose elevation is appreciably higher than sea level: Coors Field in Denver. There are zero MLB stadiums between 2000 and 5000 feet above sea level (see Figure 1). On the other hand, there are eleven Short Season A stadiums in this elevation range, and five that are higher than 4000 feet.
(Click image to enlarge.)
2. Roster turnover. Even if data are collected over many seasons, offensive output on a major league team is often skewed by a small number of prolific hitters. Likewise, home-run totals can be depressed by a strong core of ground-ball pitchers who may be on the roster for years, making it difficult to separate stadium effects from the effects of a few players with great ability. Even if only players from the visiting teams are considered when compiling statistics on home run production at Coors Field, it is still difficult to assess whether this correction is working since Coors Field is the only high-elevation stadium in the majors.
Short Season and Rookie League teams have an almost entirely different roster each season. When several seasons are analyzed, the effects of a particularly strong batter or pitcher do not influence the results significantly. Furthermore, exceptionally talented players do not spend very much time at the Short Season/Rookie level in professional baseball, so what effects their presence might have are mitigated.
3. Stadium dimensions. The stadiums in this study have reasonably uniform outfield dimensions. (No Green Monster! No Tal’s Hill in center field!) Notable exceptions are Calfee Park in Pulaski, Virginia, whose right field corner is only 301 feet from home plate but has a 19-foot wall, and Scotiabank Field at Nat Bailey Stadium in Vancouver, British Columbia, whose center field is only 385 feet from home plate but has a 20-foot wall. The following are average outfield dimensions for stadiums in this study: left field is 331 ± 11 ft, center field is 401 ± 9 ft, and right field is 328 ± 13 ft from home plate (See Table 1 for exact dimensions). One caveat is that all of them are open air stadiums which does mean that humidity, wind, and temperature can vary; these effects were not accounted for in this study but have been measured in the lab and calculated based on reasonable estimated values.10, 11
Table 1: Location, Elevation, and Dimensions of Minor League Stadiums
| City | Elevation | Parent | League | LF | CF | RF |
|---|---|---|---|---|---|---|
| Casper, WY | 5123 | Rockies | Pioneer | 350 | 400 | 350 |
| Orem, UT | 4734 | Angels | Pioneer | 305 | 408 | 312 |
| Idaho Falls, ID | 4705 | Royals | Pioneer | 340 | 400 | 350 |
| Ogden, UT | 4376 | Dodgers | Pioneer | 335 | 399 | 335 |
| Helena, MT | 4068 | Brewers | Pioneer | 335 | 400 | 325 |
| Great Falls, MT | 3300 | White Sox | Pioneer | 350 | 400 | 350 |
| Missoula, MT | 3232 | Diamondbacks | Pioneer | 335 | 414 | 335 |
| Billings, MT | 3153 | Cincinnati | Pioneer | 330 | 410 | 330 |
| Boise, ID | 2842 | Cubs | Northwest | 330 | 400 | 330 |
| Princeton, WV | 2460 | Rays | Appalachian | 330 | 396 | 330 |
| Bluefield, WV | 2389 | Orioles/Blue Jays | Appalachian | 335 | 365 | 335 |
| Spokane, WA | 2376 | Rangers | Northwest | 335 | 398 | 335 |
| Pulaski, VA | 1917 | Mariners | Appalachian | 338 | 405 | 301 |
| Elizabethton, TN | 1653 | Twins | Appalachian | 335 | 407 | 320 |
| Johnson City, TN | 1635 | Cardinals | Appalachian | 320 | 410 | 320 |
| Bristol, VA | 1615 | White Sox | Appalachian | 325 | 400 | 310 |
| Greeneville, TN | 1531 | Astros | Appalachian | 331 | 400 | 331 |
| Kingsport, TN | 1208 | Mets | Appalachian | 330 | 410 | 330 |
| Yakima, WA | 1066 | Diamondbacks | Northwest | 295 | 406 | 295 |
| Burlington, NC | 610 | Royals | Appalachian | 335 | 410 | 335 |
| Pasco, WA | 550 | Rockies | Northwest | 335 | 400 | 335 |
| Danville, VA | 531 | Braves | Appalachian | 330 | 400 | 330 |
| Eugene, OR | 412 | Padres | Northwest | 335 | 400 | 325 |
| Keizer, OR | 157 | Giants | Northwest | 325 | 400 | 325 |
| Everett, WA | 135 | Mariners | Northwest | 330 | 395 | 330 |
| Vancouver, BC | 13 | Blue Jays | Northwest | 335 | 385 | 335 |
METHOD
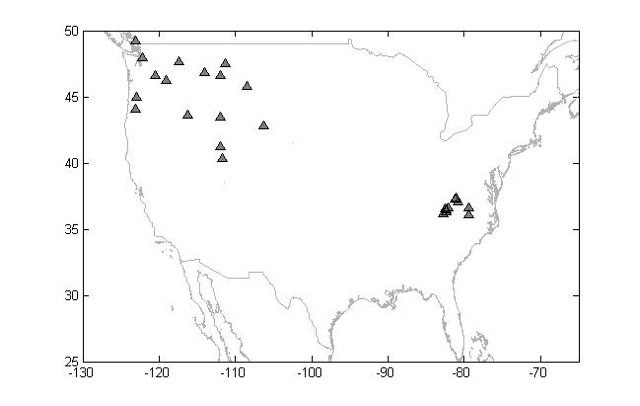
Number of home runs hit and runs scored were compiled for 26 Short Season A and Rookie League teams in the Pioneer, Northwest, and Appalachian Leagues 2008–12. The only exception is for Casper, Wyoming, in which data were compiled from 2007 through 2011 because that franchise moved to Grand Junction, Colorado, after the 2011 season. Using data from 2007 for Casper ensured that five seasons’ worth of data were recorded at each location. These represent 4802 total box scores. Number of hits, walks, and errors were compiled for one season’s worth of data at each of the same stadiums (938 total box scores). See Figure 2 for a map of the locations of stadiums in this study.
(Click image to enlarge.)
The 26 stadiums in this study range in elevation from 13 feet above sea level (Vancouver, British Columbia) to 5,150 feet above sea level (Casper, Wyoming). Data from at least 150 normalized games per stadium were collected (minimum was 155.5 games at Princeton, West Virginia and maximum was 196.11 at Ogden, Utah). I normalize the values of home runs, runs scored, home run fraction, hits, walks, and errors to “per game” which means 18 half-innings in which each team has nine chances to bat. This normalization thus correctly weights extra-innings games in which teams had more plate appearances, and also takes into account the fact that games postponed due to weather in all three of these leagues are most often made up with a double header in which each game only lasts 7 innings; therefore, teams have fewer chances to hit in these games. It further corrects for teams who play well at home and often only have eight chances to bat in a home game.
In the Pioneer League and Northwest League each stadium hosts about 35 actual games per regular season; the Appalachian League has a slightly shorter season: each stadium hosts about 33 regular season games. I also include playoff games in this analysis which accounts for most of the variation in number of box scores analyzed among teams in the same league. Each league’s season begins in late June and ends in early September. One minor drawback to using data from these leagues is that because they do not experience the dramatic differences in temperature and humidity experienced at MLB stadiums from early April through the end of September, we’re unable to corroborate predictions relating to those extremes with the empirical dataset from this set of stadiums.
All metrics reported in this study are with respect to the stadium where the games were played, not with respect to any one team. For example, the statistic “mean home runs per game” refers to the average number of home runs hit at that stadium by both teams combined in a normalized game consisting of 18 half-innings. Home run fraction is the number of runs scored via a home run as a fraction of the total runs scored in a normalized game. The value of the home run fraction ranges between zero (no home runs in the game) and one (every run scored via a home run).
Table 2: Stadium Data, 2008–12
| City | Elevation (feet) |
Box scores |
Normalized games |
HRs | Runs | HR fraction |
|---|---|---|---|---|---|---|
| Casper, WY | 5150 | 183 | 181.00 | 1.561 | 11.618 | 0.212 |
| Orem, UT | 4734 | 198 | 195.94 | 1.730 | 12.063 | 0.238 |
| Idaho Falls, ID | 4705 | 189 | 187.00 | 1.196 | 11.829 | 0.163 |
| Ogden, UT | 4376 | 200 | 196.11 | 2.348 | 13.514 | 0.288 |
| Helena, MT | 4068 | 192 | 192.06 | 1.487 | 10.630 | 0.230 |
| Great Falls, MT | 3300 | 198 | 194.67 | 1.104 | 10.392 | 0.173 |
| Missoula, MT | 3232 | 196 | 194.17 | 2.090 | 12.046 | 0.292 |
| Billings, MT | 3153 | 191 | 187.61 | 1.223 | 10.103 | 0.202 |
| Boise, ID | 2842 | 194 | 192.33 | 1.188 | 10.886 | 0.190 |
| Princeton, WV | 2460 | 159 | 155.50 | 1.204 | 9.016 | 0.208 |
| Bluefield, WV | 2389 | 171 | 165.00 | 1.277 | 10.276 | 0.210 |
| Spokane, WA | 2376 | 194 | 192.50 | 1.331 | 9.702 | 0.226 |
| Pulaski, VA | 1917 | 173 | 168.94 | 1.801 | 11.073 | 0.257 |
| Elizabethton, TN | 1653 | 171 | 165.61 | 2.173 | 10.939 | 0.329 |
| Johnson City, TN | 1635 | 175 | 168.67 | 1.672 | 11.000 | 0.235 |
| Bristol, VA | 1615 | 169 | 162.11 | 1.003 | 9.077 | 0.177 |
| Greeneville, TN | 1531 | 173 | 171.06 | 1.341 | 10.537 | 0.197 |
| Kingsport, TN | 1208 | 166 | 162.33 | 1.283 | 11.044 | 0.193 |
| Yakima, WA | 1066 | 192 | 191.67 | 0.703 | 9.489 | 0.129 |
| Burlington, NC | 610 | 175 | 172.78 | 1.373 | 8.960 | 0.239 |
| Pasco, WA | 550 | 193 | 191.22 | 0.588 | 8.168 | 0.116 |
| Danville, VA | 531 | 173 | 167.56 | 0.683 | 8.690 | 0.121 |
| Eugene, OR | 412 | 192 | 189.17 | 0.990 | 8.787 | 0.185 |
| Keizer, OR | 157 | 194 | 192.72 | 1.384 | 10.838 | 0.212 |
| Everett, WA | 135 | 194 | 189.28 | 1.881 | 10.233 | 0.297 |
| Vancouver, BC | 13 | 197 | 194.61 | 0.698 | 8.906 | 0.132 |
Includes city, elevation (feet above sea level) number of box scores analyzed, equivalent number of normalized games, average home runs, runs scored, and home run fraction from 2008–12. Elevation is reported based on United States Geological Survey quadrangle topographical maps at each stadium’s location. Home runs, runs scored and “home run fraction” (number of runs scored via a home run as a fraction of the total runs scored in a game) are reported as mean number per normalized game in which a normalized game is 18 half-innings played by both teams combined. Maximum and minimum values of games, home runs, runs, and home run fraction are bolded.
RESULTS
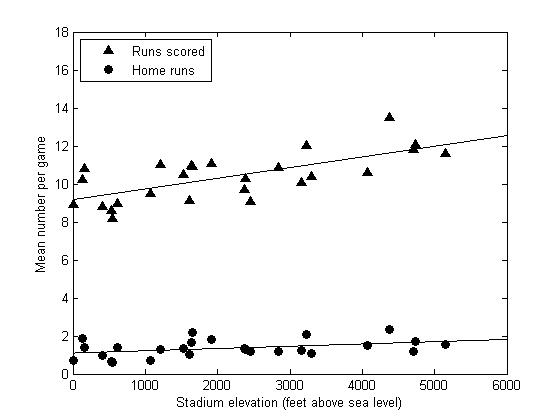
The most striking result of this study is that home runs hit per game is an even stronger function of stadium elevation than calculations based on reasonable estimates predict. A least-squares best fit to the home run data has a slope of 1.20 x 10–4 home runs/feet above sea level which translates to an extra 0.6 home runs per game at 5000 feet above sea level (Figure 3). For a season in which a stadium hosts 35 games, fans will see an extra 21 home runs per season at the very highest altitude. Robert Adair makes an educated guess with reasonable assumptions about average air density and temperature and concludes that an average player’s probability of hitting a 400-foot home run is increased by about 3.5% for every 550 feet of altitude.12 We should therefore expect about 35% more home runs at 5500 feet than at sea level assuming a linear relationship between 400-foot flies and home runs in this educated guess. The average number of home runs per game at sea level in this study is 1.10, so Adair’s calculations predict 1.49 home runs per game at 5500 feet. In fact, an extrapolation of the best fit line relating home runs to elevation using these data says that at 5500 feet we will see 1.76 home runs per game. That’s an increase of 65%, nearly double Adair’s prediction. Pre-humidor Coors Field saw an average of 3.20 home runs per game as opposed to 1.93 home runs per game by Rockies batters at other stadiums, which is an increase of 66%, just about the same as this dataset, and so we may consider Adair’s prediction of 35% to be a lower bound.
(Click image to enlarge.)
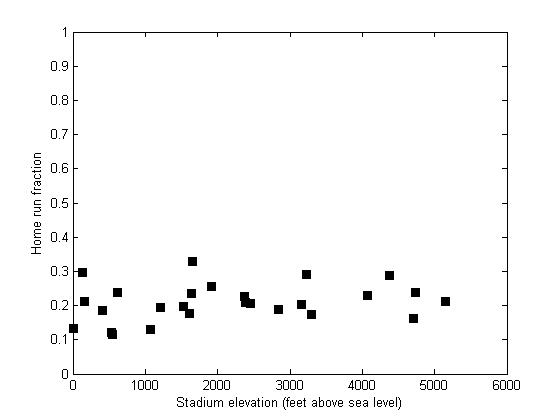
Runs scored per game also correlates strongly with elevation (see Figure 3). The runs data have appreciable scatter, but a least-squares best fit to the runs per game data has a slope of 5.61 x 10–4 runs per game per foot above sea level which translates into an extra 2.8 runs per game at 5000 feet (see Figure 3). Over the course of a season this is an extra 98 runs, quite a significant number. In fact, even though there are more home runs hit at high altitudes than calculations predict, the increase in runs scored is even more dramatic. The excess of runs scored cannot be accounted for entirely by home runs because the home run fraction does not vary with altitude (see Figure 4). The average home run fraction is 0.21 so of the extra 98 runs scored per season at 5000 feet, only 20.6 of them can be explained by extra home runs. How do we account for the other 77.4 runs? Answering this question is the topic under discussion for the rest of this paper.
(Click image to enlarge.)
Clearly, the strong relationship between runs scored and elevation means that on-base percentage is increased at high altitudes. Batters have to reach base to eventually score a run, so it makes sense to examine all the ways a hitter can reach base safely and determine which of these correlate with altitude. Home runs we have already analyzed—and in any case, home runs are a special category of hits. In general, to reach base a batter must do one of the following: hit safely, walk, reach on an error, get hit by a pitch, reach base on a fielder’s choice, be awarded first base on catcher’s interference or a dropped third strike. In practice, these last two are rare enough that there were no instances of either of them happening in the five years of data collected (4802 total box scores). Furthermore, the sample size of hit-by-pitches was too small to allow for meaningful analysis. Therefore, I limit this discussion to hits, walks, and errors.
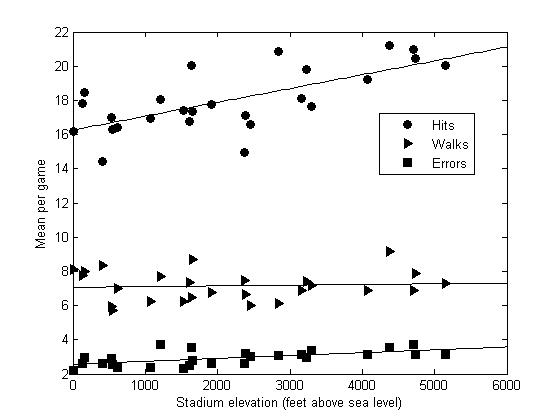
I collected one year of these data (2012 for all stadiums except 2011 for Casper, Wyoming) for each stadium. Results are given in Table 3 and plotted in Figure 5.
Table 3: Stadium Data, 2012
| City | Elevation | Box scores |
Normalized games |
Hits | Walks | Errors |
|---|---|---|---|---|---|---|
| Casper, WY | 5150 | 37 | 37.389 | 20.059 | 7.302 | 3.156 |
| Orem, UT | 4734 | 37 | 37.556 | 20.450 | 7.882 | 3.142 |
| Idaho Falls, ID | 4705 | 37 | 38.278 | 20.978 | 6.897 | 3.710 |
| Ogden, UT | 4376 | 41 | 40.278 | 21.228 | 9.137 | 3.550 |
| Helena, MT | 4068 | 37 | 37.944 | 19.212 | 6.905 | 3.163 |
| Great Falls, MT | 3300 | 39 | 39.444 | 17.645 | 7.200 | 3.372 |
| Missoula, MT | 3232 | 39 | 40.000 | 19.825 | 7.400 | 2.975 |
| Billings, MT | 3153 | 37 | 36.611 | 18.109 | 6.883 | 3.168 |
| Boise, ID | 2842 | 40 | 40.333 | 20.876 | 6.099 | 3.074 |
| Princeton, WV | 2460 | 32 | 32.333 | 16.608 | 6.000 | 3.000 |
| Bluefield, WV | 2389 | 30 | 28.833 | 17.133 | 6.624 | 3.191 |
| Spokane, WA | 2376 | 37 | 38.722 | 14.953 | 7.463 | 2.634 |
| Pulaski, VA | 1917 | 32 | 33.778 | 17.734 | 6.750 | 2.635 |
| Elizabethton, TN | 1653 | 34 | 33.722 | 17.377 | 8.689 | 2.579 |
| Johnson City, TN | 1635 | 34 | 32.722 | 20.048 | 6.448 | 3.545 |
| Bristol, VA | 1615 | 32 | 30.667 | 16.793 | 7.337 | 2.511 |
| Greeneville, TN | 1531 | 34 | 34.889 | 17.398 | 6.248 | 2.293 |
| Kingsport, TN | 1208 | 31 | 30.389 | 18.033 | 7.700 | 3.718 |
| Yakima, WA | 1066 | 39 | 39.778 | 16.970 | 6.235 | 2.363 |
| Burlington, NC | 610 | 37 | 37.167 | 16.386 | 6.996 | 2.368 |
| Pasco, WA | 550 | 37 | 37.778 | 16.279 | 5.718 | 2.541 |
| Danville, VA | 531 | 34 | 32.667 | 17.020 | 5.939 | 2.908 |
| Eugene, OR | 412 | 37 | 37.944 | 14.416 | 8.354 | 2.635 |
| Keizer, OR | 157 | 37 | 38.667 | 18.440 | 8.017 | 2.974 |
| Everett, OR | 135 | 38 | 37.944 | 17.842 | 7.775 | 2.635 |
| Vancouver, BC | 13 | 39 | 38.444 | 16.205 | 8.116 | 2.211 |
City, elevation (feet above sea level) number of box scores analyzed, equivalent number of normalized games, mean number of hits, walks, and errors per normalized game in the 2012 season. Elevation is reported based on United States Geological Survey quadrangle topographical maps at each stadium’s location. Hits, walks and errors are reported as mean number per normalized game at that stadium in which a normalized game is 18 half-innings played by both teams combined. Maximum and minimum values of hits, walks, and errors are bolded.
The slope of the least squares best fit line to hits per normalized game as a function of elevation (filled circles in Figure 5) is 8.09 x 10–4 hits/foot. At 5000 feet that translates to an average of four more hits per game than at sea level. For a single season in which a stadium hosts 35 home games, fans will see 140 additional hits per season at 5000 feet compared to what they would see at sea level. The slope of the best fit of walks per game as a function of elevation is 4.14 x 10–5 walks/foot which translates to 0.2 extra walks per game at 5000 feet and therefore 7.2 extra walks per season. The best fit line relating errors per game to elevation has a slope of 1.68 x 10–4 errors/foot, so at 5000 feet that is 0.8 extra errors per game and 28 extra errors per season.
(Click image to enlarge.)
DISCUSSION
Results are unequivocal. There are more home runs hit at high altitude than low altitude, and nearly double the calculated prediction. However, Adair’s prediction of 35% more home runs at 5500 feet is most likely a lower bound. Note that when home runs and runs scored are plotted on the same axes, it is quite obvious that runs scored is of far more practical significance in terms of the correlation with altitude. The excess number of runs scored that cannot be accounted for entirely by home runs is startlingly large (Figure 3).
Number of hits strongly correlates with elevation, and so does number of errors. On the other hand, number of walks varies very little. So we know there are more runs scored at high altitudes, but the more interesting question to explore is this: Why are there more runs scored at higher elevation that are not entirely due to home runs being hit more often there? There are a number of reasonable possibilities, none of which are mutually exclusive, many of which can be tested with regard to this empirical dataset. These possibilities fall under four main categories: pitching, hitting, fielding, and psychology.
1. Pitching. Numerical models predict that a 10 percent drop in air density decreases the break of a curveball by as much as nine percent.13 Curveballs that don’t curve and breaking balls that don’t break fool fewer hitters, leading to more hits. This scenario leads to higher on-base percentage without needing home runs to do it, which is what we require to be consistent with our dataset. This dataset further indicates that walks do not contribute to the higher on base percentage at high altitudes (Figure 5). This observation is also not inconsistent with computer models that show little if any horizontal change in the trajectory of pitched balls, but significant changes in vertical location.14 A pitcher who is most likely to miss his spot by leaving a pitch in the strike zone (missing high) when he intended not to throw a strike would throw more hittable pitches without increasing the number of walks, consistent with these data.
A pitcher who consistently misses the strike zone in the horizontal dimension has his own mechanics or psychology to blame rather than the altitude of the stadium. What I mean by this is that pitchers who put a left-to-right or right-to-left curve on the ball should not be affected by the altitude of the stadium. If they are, it is probably due to psychology (see point 4 below). Pitchers who rely on a pitch that breaks out of the strike zone will have the most trouble because their pitches may tend to come in high and hittable.
2. Hitting. A batted ball hit at high altitude travels farther and gets to the fielders more quickly.15 Computer simulations have shown that the increase in distance traveled as a function of altitude is greater for line drives than for home run balls, the majority of which are fly balls (Bahill, et. al. studied home runs in specific). We presume this is because the trajectory of a line drive maximizes the reduction in drag that comes from reduced air density while minimizing the reduction in the Magnus coefficient that decreases lift.16 On the other hand, more recent work involving statistical analysis of batted balls during actual major league baseball games using the TrackMan doppler system shows that line drives are affected less than fly balls at high temperatures, which can be taken as a proxy for high altitude since the effect on projectile motion of a baseball is the same for increased temperatures and increased elevation.17
My study cannot speak to the conflict between these two previous studies as I can only state that more hits are recorded at high altitude stadiums, not whether those were bloops, short flies, or line drives. In whatever way it happens, an increase in non-home run hits that is more dramatic than the increase in home runs is perfectly consistent with this dataset. If fielders play back expecting batted balls to sail, then more bloops can drop in front of them for hits, consistent with this dataset and consistent with Alan Nathan’s analysis using the TrackMan system. A line drive to an out-of-position player who can’t get to the ball fast enough is consistent with this dataset and consistent with Bahill et al.’s simulations. Further analysis of batted balls during games at the ball parks in this study may be warranted to determine which of these two scenarios is more common.
An educated guess also is that high altitudes have more detrimental effects on aerobic activities (running) than anaerobic activities (swinging a bat), further compounding the likelihood of an average batter collecting more hits at high elevation because the fielders can’t get to the ball fast enough.
3. Fielding. Thrown balls are more likely to sail at higher elevation, increasing the number of errors. If a player is slightly out of position or loses track of a fly ball, he will have less time to correct his mistake because the ball will arrive more quickly at high elevation. If a player doesn’t get to a ball at all, that will probably be scored a hit (see point 2 above) but if he just barely gets there and the ball glances off his glove, that will most likely be an error, even though the real culprit is the enhanced flight of the ball at altitude. Both sailing throws and missed catches will lead to more men on base due to errors, again consistent with this dataset.
4. Psychology. The possibilities examined so far, namely pitching, hitting, and fielding, are mutually consistent and probably all contribute to the enhanced on-base percentage observed at high altitude stadiums. In addition, I believe there is a fourth important factor, and that is the psychology of the baseball players. Confirmation bias—the practice of unconsciously collecting a mental dataset that is consistent with pre-conceived notion about a topic—is a well-known human tendency and has been studied in fields as diverse as science and intelligence analysis.18 In practice, it means that people have a tendency to remember observations that agree with what they already think is true and ignore all data to the contrary.
Confirmation bias can manifest itself in a variety of ways in a baseball game, especially for inexperienced players who populate the Short Season A rosters. Outfielders “know” that there will be more home runs at high elevation so they play back farther, which allows hitters to dump singles in front of them all game long. Pitchers “know” their curveball doesn’t work well at altitude so they pitch tentatively or leave balls over the middle of the plate that they intended to break out of the strike zone resulting in more hits (but not necessarily more walks). Batters “know” they will hit better at high altitude and arrive at the plate full of confidence, resulting in better batting performance. All of these scenarios are likely, and they can’t be easily separated from the physics of the flight of a batted ball with the dataset at hand, but confirmation bias can help to explain why offensive statistics are even more enhanced than calculations predict they should be.
It would be an interesting follow-up to take an overhead photo of each field in this study at the end of the season to see whether there is a significant difference in the distance between the outfield fence and the bare spots where the outfielders prefer to play that correlates to the elevation of the stadium. Another psychological point that is impossible to disentangle from the effects of stadium elevation is player fatigue. High altitude is fatiguing by itself, and the stadiums at the highest elevations are also the farthest away from each other (see Figure 1). Players in the Pioneer League spend long bus rides between series to get from one town to another, and this probably has an effect on performance. A useful follow-up study might try to isolate this effect by examining the differences in game statistics between the first game of a home stand and later games. If the “travel fatigue effect” is significant, than we might expect the first game of a home stand to involve the biggest enhancement to on-base percentage.
One might also expect that a league in which some teams are at sea level and some are at very high elevation might provide clues about psychology because players would have to recalibrate often during a season as they travel back and forth between low and high elevations. The California League (high A) is a good candidate for a follow up study in this regard because there are some low and high stadiums. The Pacific Coast League (AAA) has the biggest vertical relief with some stadiums at sea level and the Albuquerque Isotopes playing at about 5300 feet, but collecting data from any league higher than class A ball will taint the analysis with roster effects that are probably too important to ignore.
CONCLUSIONS
Knowing which factors are most likely to contribute to high offensive output would help scouts, coaches and managers select and mentor the players who are going to play in stadiums located at high elevations. In this study it is evident that all the factors contributing to on-base percentage are enhanced as a function of stadium altitude, with the exception of walks.
Is it important to limit the offense at high altitude stadiums? An argument may be made that the psyches of young pitchers could be affected adversely by playing in conditions that lead to so much offense. An equally strong counter-argument could be made that the caliber of fielding might be improved if players are forced into situations where they need to track the trajectory of a ball in flight and get to it faster. This can be negated if they have to compensate by using throwing mechanics that are different at different stadiums.
Crucially, this dataset shows that merely moving the outfield walls back will not decrease offense: most of the excess runs scored come from additional base hits and fielding errors as opposed to home runs. All those in attendance on June 18, 2012, in Idaho Falls, Idaho who watched the hometown Chukars defeat the Orem Owlz 16–14 can attest to this. Of the 30 runs scored in the game, only two can be attributed to home runs—both solo shots. However, that game featured 29 hits, nine errors, and 14 walks between the two teams. This example is on the high end of offensive output at high elevations in this dataset, but is by no means an outlier.
Keeping the walls in the same place but building them higher is an option that can limit home runs and might keep the outfielders from having to play so far back that base hits drop safely in front of them throughout the game. Fielders will be forced to pick up the additional skill of fielding off a high outfield wall that collects all the extra line drive hits. However, at present not a single team in this data set is affiliated with the Red Sox, who arguably have the strongest need to develop this skill, given the particulars of Fenway Park. Storing the balls in a humidor as has been done at Coors Field since 2002 has likely limited the number of home runs there.19, 20 Building higher outfield walls might be a more cost-effective solution at minor league ballparks, if a solution is deemed necessary.
ELIZA RICHARDSON is a seismologist by training and an associate professor at Penn State University. She grew up in Blacksburg, Virginia, and some of her earliest memories are listening to the Cardinals on KMOX with her dad, who is a lifelong Cardinals fan. When not throwing batting practice to their five children or discussing baseball stats, Eliza and her husband are avid homebrewers.
Acknowledgements
I thank George Skornickel and the rest of the SABR Forbes Field chapter for encouraging feedback and speculations regarding this research. Thanks also to the past and present members of the PSU Rock Mechanics lab for the discussions and the beer.
Notes
1 Robert K. Adair, The Physics of Baseball (New York: HarperCollins, 2002).
2 Cliff Frohlich, “Aerodynamic drag crisis and its possible effect on the flight of baseballs,” American Journal of Physics, 52 (1984): 325–34.
3 A. Terry Bahill, David G. Baldwin, and John S. Ramberg, “Effects of Altitude and Atmospheric Conditions on the Flight of a Baseball,” International Journal of Sports Science and Engineering, 3 (2009): 109–28.
4 David T. Kagan and D. Atkinson, “The coefficient of restitution of baseballs as a function of relative humidity,” Physics Teacher, 42 (2004): 330–3.
5 Alan M. Nathan, J. Hopkins, L. Chong and H. Kaczmarski, “The effect of spin on the flight of a baseball,” SABR 36 convention, Seattle, June 2006.
6 Frederick Chambers, Brian Page and Clyde Zaidins, “Atmosphere, weather, and baseball: how much farther do baseballs really fly at Denver’s Coors Field?” The Professional Geographer, 55 (2003): 491–508.
7 Adair, 19.
8 Adair, 21.
9 Edmund R. Meyer and John L. Bohn, “Influence of a humidor on the aerodynamics of baseballs,” American Journal of Physics, 76 (2008): 1015–21.
10 Kagan and Atkinson.
11 Adair, 20–22.
12 Adair, 27.
13 Bahill et al.
14 Bahill et al.
15 Adair, 21.
16 Bahill et al.
17 Alan M. Nathan, “What New Technologies Are Teaching Us About the Game of Baseball,” http://baseball.physics.illinois.edu/TrackingTechnologiesBaseball.pdf, (2012).
18 Richards J. Heuer, Psychology of Intelligence Analysis, (Central Intelligence Agency, Washington, D.C., 1999).
19 Meyer and Bohn.
20 Alan M. Nathan, Lloyd V. Smith, Warren L. Faber and Daniel A. Russell, “Corked Bats, Juiced Balls, and Humidors: The Physics of Cheating in Baseball,” American Journal of Physics, 79 (2011): 575–80.