Should Teams Walk or Pitch to Barry Bonds?
This article was written by Jerome P. Reiter
This article was published in 2003 Baseball Research Journal
In 2001, Barry Bonds of the San Francisco Giants had arguably the greatest individual season in the history of major league baseball. He set the record for home runs in a season with 73. He hit for the highest slugging percentage ever at .863, breaking Babe Ruth’s 1920 mark of.847. He knocked in 137 runs, good for fourth best in the National League, and his batting average was .328, good for seventh best in the league. Bonds achieved these gaudy statistics despite being walked by opposing pitchers a major league record 177 times, besting Ruth’s 1923 record of 170. Not surprisingly, Bonds was voted the Most Valuable Player in the National League by an overwhelming margin. It was the fourth time he won the MVP award.
Bonds did not slow down in the next year. He began the 2002 campaign with an incredible display of power, hitting five home runs in the Giants’ first four games. His year-end statistics were remarkable: a major league-leading .370 batting average, a National League second-best 46 home runs, and a National League sixth-best 110 runs batted in. He reached base in 58.2% of his plate appearances, eclipsing the previous record of 55.1% set by Ted Williams in 1941. He passed Frank Robinson for fourth all-time in career home runs, with only Willie Mays, Babe Ruth, and Hank Aaron ahead of him. Perhaps most amazingly, Bonds finished with 198 walks, shattering the record he set last season. Once again Bonds was voted MVP in the NL.
Bonds maintained this remarkable productivity in 2003, despite missing about 30 games. He was among the top three in batting average (.341) and home runs (45) in the National League, and he had a slugging percentage (.749) 82 points higher than Albert Pujols’ second-best mark. Bonds hit his 45 home runs in 390 official at-bats; in contrast, the National League home run champion, Jim Thome, needed 587 official at-bats to hit 47 home runs. As Bonds’ low at-bat total indicates, he was again walked with unusual frequency: he finished with 148 walks, averaging more than one per game. Bonds was voted MVP for the third straight year, the first player to win three consecutively.
The inflated walk totals in 2001, 2002, and 2003 reflect increased use of a strategy for dealing with Bonds’ awesome power, namely not to let him have a chance to hit the baseball and instead to walk him. Why risk pitching to a player who averaged one home run every 6.5 at-bats in 2001 and every 8.7 at-bats in 2002 and 2003? However, walking Bonds is not fail safe. Putting him on base via walk could actually help the Giants since runners on base greatly increase a team’s chance of scoring runs. Plus, as prolific a batter as he is, over his career Bonds has made an out roughly 70% of the times he is not walked. Why not pitch to him since outs are the most likely outcome?
Thus, we are confronted with an interesting question of baseball strategy: is it better to walk Barry Bonds or to pitch to him? Clearly, the answer depends on the game situation when Bonds steps to the plate. For example, walking Bonds has different consequences when there are zero outs and runners on first and second as opposed to when there are two outs and a runner on third. The answer also depends on the outcomes the opposing manager is concerned about. The manager who seeks to prevent even a single run – for example in late or extra-inning situations in which one run can result in a lost game – evaluates walks differently than does the manager who will concede one run to reduce the possibility of multiple runs.
In this article, I examined data from the 2001, 2002, and 2003 seasons to investigate if and when it is a better strategy to walk rather than pitch to Barry Bonds. I focused primarily on two game situations: when there is no one on base, and when there is a player on first base only. The conclusions suggested by the data are somewhat surprising: in these two situations, walking Bonds generally is not more effective at preventing runs than letting him hit. In fact, data even suggest that it is preferable in some situations to let Bonds swing away.
Data Used in Analyses
To assess the two strategies, I examined data on Bonds’ plate appearances in the 2001 through 2003 seasons. The data were retrieved from www.cbs.sportsline.com, which has links to pitch-by-pitch game logs for each game in 2001, 2002, and 2003. Data for a few games were unavailable because of invalid web links; these games are excluded from the analyses. This should not skew results since these games are missing completely at random, that is, they are missing for reasons unrelated to the variables measured.
Some Characteristics of Bonds’ Plate Appearances
There are 24 possible game situations when a player steps into the batter’s box. These are obtained by crossing the three possible out values and the eight possible configurations of players on base. Table 1 displays the number of walks and plate appearances by Bonds in 2001, 2002, and 2003 in each of these 24 game situations. In this table, and for all analyses, intentional and unintentional walks and hit-by-pitches are included in the walk totals.
In most games in 2001, Bonds batted third in the San Francisco Giants batting order, so that he often came up with two outs and the bases empty or with one out and a runner on first base. In 2002 and 2003, Bonds typically batted fourth in the order, often leading off innings or batting with runners on base and two outs. In all three seasons, most of Bonds’ walks were issued with two outs. This is understandable: with two outs, some managers feared Bonds’ ability to get extra base hits more than his teammates’ ability to score him from first base.
Managers were more reluctant to walk Bonds with zero or one outs, perhaps because multiple players had the chance to advance him home. Bonds walked most frequently when runners were in scoring positions and first base was unoccupied. Walking players in these situations is a common baseball strategy.
Game situations other than those in the “None On” and “First Only” categories have few observations. Hence, the analyses that follow focus primarily on the None On and First Only categories.
Bonds is in the heart of the Giants batting order so that we expect innings in which he appears at the plate to be the most productive for the team. The relevant outcome is not the total number of runs in each inning, rather it is the total number of runs scored in the inning after the first pitch to Bonds. Hence, for purposes of analyses, runs in an inning is redefined to be the num ber of players crossing the plate in that inning. Figure 1 shows the frequencies of the run totals for all innings in which Bonds stepped to the plate. In more than 60% of the innings, the team scores zero runs. Scoring more than two runs in an inning is rare. This suggests that fear of large run totals should not be a strong factor in the decision to walk or pitch to Bonds.
Walking Bonds to Prevent the Giants From Scoring
When games are close in late or extra innings, the goal is to not allow runs. This goal motivates the primary question: does walking rather than pitching to Barry Bonds reduce the chance that at least one run scores?
For some game situations, baseball strategy dictates that walking Bonds is the smart choice. These include the situations in which first base is unoccupied and there are runners in scoring positions. Consider the situations on an out-by-out basis. With two outs, walking Bonds is preferable since he has a higher batting average than those players batting immediately after him. That is, Bonds is more likely to get a hit, thereby driving home the run than those other players. With one out, walking Bonds sets up a double play that potentially can end the inning without any runs scoring. With zero outs, walking Bonds sets up force plays that prevent the lead runner from advancing further.
For other situations, it is clear that a walk is not the smart choice. When the bases are loaded, a walk automatically gives the Giants a run. With runners on first and second and less than two outs, a walk advances a runner to third base, where he can score on a fly out or a well-placed ground out.
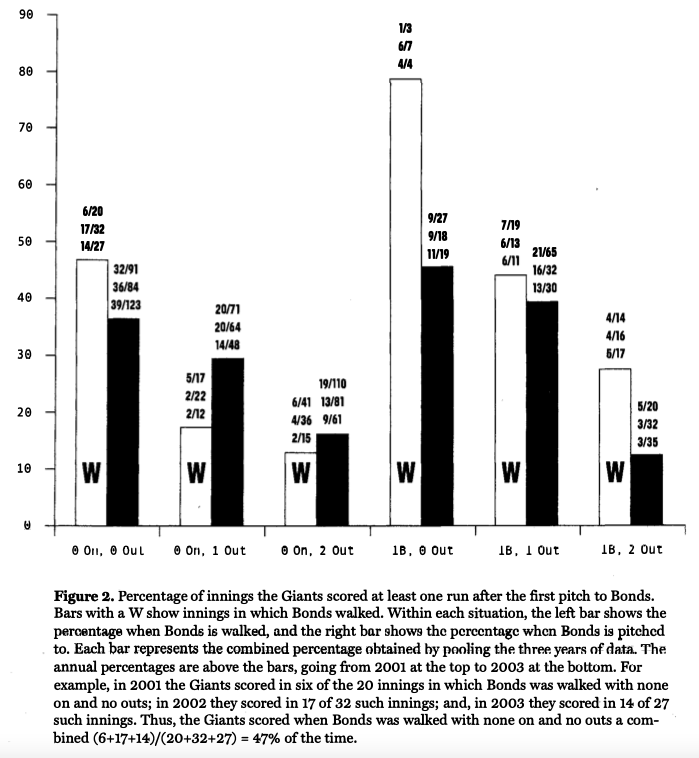
For the remaining situations, it is not clear from baseball strategy whether walking or pitching to Bonds is the smart choice. Hence, it is useful to examine data for evidence of the success of one strategy over the other. This can be done by comparing the percentages of innings in which the Giants score at least one run when Bonds walks versus when he bats. This comparison is displayed in Figure 2 for the None On and First Only situations.
For comparisons, all three years of data are combined in single percentages. Pooling the data across years simplifies comparisons of the strategies. Additionally, the combined percentages are based on larger numbers of innings than the annual percentages, which improves our ability to differentiate the effectiveness of the strategies. A drawback to pooling the data is that it masks any differences across years.
At first glance, the combined percentages suggest competitive advantages for each strategy. With none on and at least one out, walking Bonds seems more effective than pitching to him. This may be because, in these situations, the risk that Bonds hits a home run outweighs the risk that he scores when put on first base. With none on and no outs, walking Bonds seems less effective than pitching to him. This suggests that avoiding Bonds’ home run power is outweighed by beginning an inning with a free pass. With one man on base, pitching to Bonds seems to be the better strategy. The walk advances the runner on first to scoring position, and the risk of that runner scoring may outweigh the risk of Bonds driving in the runner from first.
These percentages are based on a limited number of plate appearances. Suppose there is no difference in the true probabilities of the Giants scoring when Bonds walks or hits. Could these apparent differences be plausibly explained by random chance? To answer this question, we conceive of a hypothetical population of Bonds’ plate appearances under the same conditions that existed in 2001 through 2003, and we consider the plate appearances in 2001, 2002, and 2003 a random sample from this hypothetical population. Under this framework, the answer to our question is “not likely” for some situations and “entirely plausible” for others. When we combine the three years of data, the p-values for two-tailed statistical hypothesis tests are small for None On Zero Outs (p-value = 0.08), for None On One Out (p-value = .04), and for First Only Two Outs (p-value = .04). Hence, if walking and pitching to Bonds are equally effective, in these three situations we expect to see differences in the combined percentages as large (or larger) than those in 2001 through 2003 at most 8% of the time, indicating chance error is not a likely explanation of these differences. The p-values associated with the tests for None On Two Outs and for First Only One Out are both much greater than 0.1 o, indicating walking and pitching to Bonds in these situations could be equally effective. There is little data for First Only Zero Outs, although a simple examination of the differences suggests pitching to Bonds is a better option than walking him in that scenario.
Before accepting these conclusions, we should make sure that our comparisons are fair to both strategies. That is, up to the point when Bonds steps to the plate, the innings in which he walks should have similar characteristics to those in which he hits. In general, when comparing two strategies, fairness can be assured by assigning the strategies to the experimental units at random. We do not have this setup when analyzing the data. Decisions to walk or pitch to Bonds were made by managers rather than at random. Hence, we have to check whether the walk-innings differ from the hit innings in ways that could affect the chances of scoring runs.
Other than game situation, the primary variable that affects the number of runs scored is the opposing pitcher’s quality. Weak pitchers are likely to give up more runs than strong pitchers, regardless of whether they walk or pitch to Bonds. A pitcher’s quality can be measured by his earned run average (ERA) over his career, which roughly equals the total number of all runs allowed by the pitcher divided by the number of innings he has pitched. Based on investigations within each game situation, the distributions of ERA are similar for the innings Bonds walks and innings he does not walk. An example of this similarity is displayed in Figure 3, which shows distributions of opposing pitchers’ ERAs for None On situations in 2003. The overlap in the distributions for walk-innings and hit-innings is reproduced in other game situations and years. Hence, any effects of ERA on runs are approximately equally present in the side-by-side percentages of Figure 2. The comparison is fair with respect to ERA.
Another potentially important factor in the decision to walk or face Bonds is the quality of the player hitting after Bonds. In roughly 85% of his at-bats in 2001, Bonds was followed by Jeff Kent, and walks were similarly distributed in games when Kent or someone else batted after Bonds. In 2002, Kent followed in roughly 52% of plate appearances; Benito Santiago followed in roughly 28% of plate appearances; Reggie Sanders followed in roughly 18% of plate appearances; and, other players accounted for the remaining 2%. Bonds walked in roughly 33% of his at-bats when followed by Kent, 33% when followed by Santiago, and 37% when followed by Sanders.
In 2003, Bonds was followed by Edgardo Alfonso in roughly 28% of plate appearances, by Jose Cruz Jr. in roughly 30% of appearances, by Benito Santiago in roughly 29% of appearances, and by a mix of others in 13% of appearances. Bonds walked 25% of the Lime when followed by Alfonso, 31% of the time when followed by Cruz Jr., 29% of the time when followed by Santiago, and 30% of the time when followed by others.
Based on the three years of data, we can conclude that Bonds was walked with similar frequency regardless of who was on deck. Hence, comparisons of walk-innings and hit-innings within each game situation should not be affected greatly by differences in the players batting after Bonds.
Other variables examined include whether the game is in San Francisco or at other stadiums, the score, the inning, and the game number in the season. For these variables, there are one or two game situations for which the variables’ distributions differ in the walk innings and the hit-innings. These differences should have minimal effect on the comparisons because these variables do not have strong relationships with the probability of scoring runs. Players of Bonds’ caliber, and those who bat after him, try equally hard to score runs regardless of the stage of the game and the time of the season.
Hence, the conclusions stand. When the objective is to prevent any runs from scoring, the data suggest walking Bonds may be preferable when there is no one on and at least one out, and pitching to him may be preferable when there is a runner on first base or when Bonds leads off an inning.
Does Walking Bonds Help Avoid Big Innings?
Does walking Bonds have an effect on the chance of scoring runs in general? That is, do we expect bigger run totals when Bonds is walked as opposed to when he hits? We next use the data to investigate this question for the None On and First Only game situations.
Let the variable y represent the number of runs scored in an inning. For example, y=2 means two runs are scored. Ideally, we’d know the probability the Giants score y runs for each value of y in each game situation under both strategies, so we could compare the two strategies in any situation by comparing their probabilities. Of course, we don’t know these probabilities, so we use the data to learn about them.
As Figure 1 shows, it is relatively rare that y>3. In fact, y>3 for only about 1 % of all innings in the None On situation and about 3% of all innings in the First Only situation. This suggests that we can simplify analyses without losing much information by collapsing runs into four categories: y=0, y=1, y=2, and y≥3.
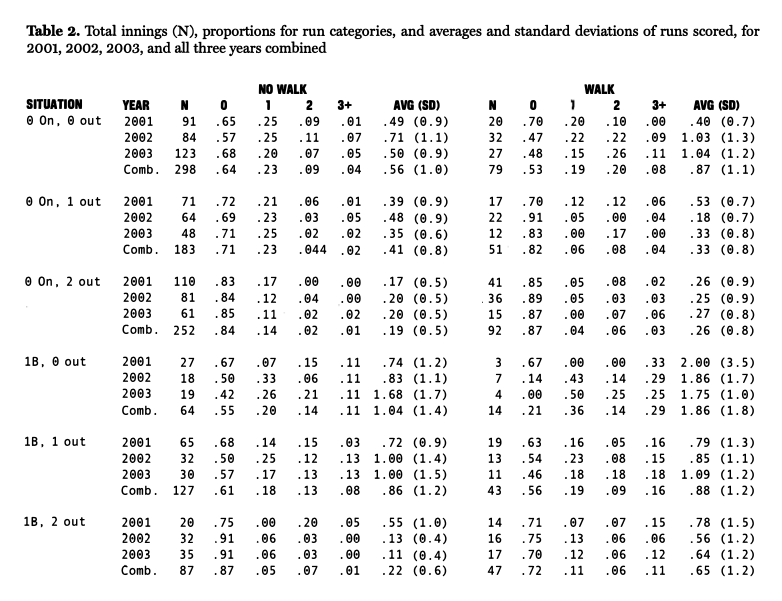
Natural estimates of the probabilities for these four run categories are the proportions of runs that fall in each category in Bonds’ combined plate appearances from 2001, 2002, and 2003. These proportions are displayed in Table 2. The table also includes the averages and standard deviations of the number of runs.
(Click image to enlarge)
For positive run categories, there is an interesting trend in the data. Let x be the number of runners on base when Bonds steps to the plate. When Bonds hits, the Giants are more likely to score exactly (x+1) runs than when he walks. On the other hand, when Bonds walks, the Giants are more likely to score (x+2) or more runs than when he hits. The averages of runs are typically as small or even smaller when Bonds hits than when he walks, the one exception being when the bases are empty with one out. Overall, these patterns suggest that it might be preferable to pitch to Bonds rather than to walk him in the None On and First Only situations, although opposing teams face risks when using either strategy.
As before, we should consider random variation when interpreting these sample proportions and sample averages. Suppose there is no difference in the effectiveness of walking or pitching to Barry Bonds in reality. Could the differences between walk-innings and hit-innings observed in 2001-2003 be plausibly explained by random chance? Let’s again conceive of Bonds’ combined 2001-2003 plate appearances as a random sample from a hypothetical population of his plate appearances under the current conditions in the league. We seek to learn about the differences in average runs in this hypothetical population when walking versus pitching to Bonds.
For the game situations (i) a runner on first only and zero outs and (ii) a runner on first only and two outs, the p-values for two-tailed statistical hypothesis tests are both around 0.02, small enough values to cast doubt on chance error as an explanation for the differences in the sample averages in these situations. For these situations, the data provide evidence that favors pitching to Bonds. For the other game situations, the p-values of the two-tailed statistical hypothesis tests are all greater than .10, making it hard to rule out chance errors as explanations of the differences in the sample averages. For these other situations, there is not enough evidence to determine conclusively that one strategy results in fewer runs on average than the other strategy does.
Concluding Remarks
There have been an incredible number of walks issued to Barry Bonds in the last three years. Given his prodigious home run power, it is understandable why managers fear pitching to him. However, the data from 2001 through 2003 suggest that there is little difference in opposing teams’ ability to prevent runs when walking Bonds versus when letting him hit. In fact, the data suggest that it may be better to pitch to Bonds than to walk him in some game situations.
JERRY REITER is an assistant professor at the Institute of Statistics and Decision Sciences at Duke University. His areas of research include statistics in government, social sciences, and sports. He is an avid Red Sox fan and doesn’t believe in The Curse.
Acknowledgments
The author thanks David Tung, John Lee, and Jonathan Bigelow for assistance with collecting the data.