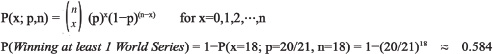The Symbiotic Relationship of Individual and Team Success

Ken Griffey Jr. is one of the all-time greats who never played on a championship team. (SEATTLE MARINERS)

 

Success comes in many forms—from individual exploits to team accomplishments and everything in between. Audiences watch teams and players winning titles or toppling records and live vicariously through these experiences. Baseball fans may value determination and perseverance in the face of failure, while hoping that the next at bat, pitch, or season might mark the beginning of success. But despite the many metrics that can be used to quantify it, impressions of what is considered “successful” for a player or team can be highly subjective. The degree to which fans are primed by messages of success from professional baseball raises two important questions: What constitutes success in baseball? And how interconnected are the various measures and metrics of success?

A good way to begin an analysis of this topic is by exploring the National Baseball Hall of Fame. The Hall of Fame seeks to recognize personal success and now honors an elite club of 333 members who comprise some of the greatest individuals baseball has ever known.1 These individuals range from players and managers to umpires and executives. Induction into the Hall of Fame in Cooperstown, New York, is considered by many to be the highest individual achievement in baseball. While methods have varied historically, induction is currently determined by rules of general eligibility and a voting committee. The current rules stipulate that players must have played in a minimum of ten seasons, been retired for at least five seasons, and received approval from a screening committee.2

While it is easy for screening committees to ratify a candidate on the basis of seasons played, the voting committee undertakes the much more difficult task of evaluating a player’s skill, talent, and contribution to their teams’ success.3 Individual players must have enjoyed “successful” careers in order to be inducted into the Hall of Fame. One subjective assumption that is often made is that career success is evidenced by team accomplishments such as World Series rings. In the minds of many, World Series titles are indicators of superior—potentially legendary—athletes. However, all-time greats such as Ted Williams, Ty Cobb, George Sisler, and Ken Griffey Jr. have never captured the elusive championship.4

This project aims to examine Hall of Fame players and World Series championships to understand how players become Hall of Famers without playing on a World Series-winning team, and conversely, how the World Series can be won with or without extraordinary players, and to determine if there is a relationship between individual success and team success. Understanding how and why World Series titles influence individual placement in the Hall of Fame is useful for recognizing what promotes success more broadly. This project will probe possible explanations for why, if Hall of Fame induction is an individual rather than team accomplishment, there are a greater number of Hall of Fame players who have won a World Series than have not. Is the subjective ideal of “success” responsible?

METHODOLOGY AND RESULTS

The initial proportion of Hall of Fame players who won a World Series was calculated from numbers given by the National Baseball Hall of Fame. As of 2020, there are 144 members in the Hall of Fame who have played on a World Series champion. There are a total of 235 players inducted in the Hall of Fame from the American and National Leagues. To ensure a fair and accurate comparison between eras, we looked at World Series that occurred from 1903 to present. Therefore, of these 235 MLB players, only 218 played in a season during this timespan. Thus, p of 144/218 (p » 0.66) was used for statistical calculations.

The expected proportion of Hall of Fame players to win a World Series was calculated using the average career length of a Hall of Fame player and assuming World Series championships were uniformly distributed among MLB teams. The average career length for a Hall of Fame player was calculated to be 18 seasons. The average number of teams in the MLB during a World Series season was calculated to be 21 teams. (More information on how p was calculated can be found in the Appendix.)

The Binomial test was performed using values displayed in Table 1. A significance level of α = 0.05 was used. Thus, the number of Hall of Fame players who have won a World Series is significantly greater than expected because the observed p-value of 0.0129 is less than α.

 

Table 1. Hall of Famers to Win World Series Binomial Test

(Click image to enlarge)

 

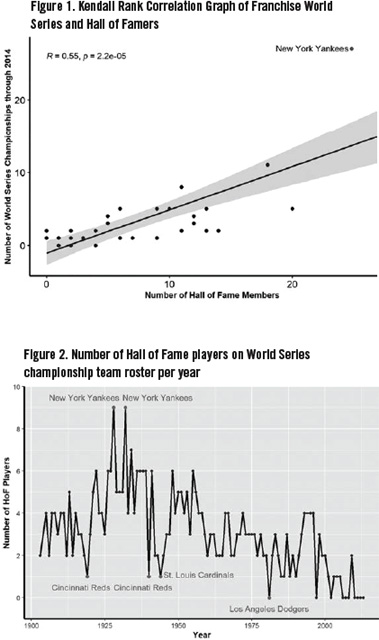
Variables that might explain the increase in the number of Hall of Fame players who have won a World Series were investigated. A Kendall rank correlation test was used to analyze the relationship between the number of World Series championships an MLB team had and the respective number of Hall of Fame members that correspond with that MLB team.5–6 This correlation is displayed by Figure 1.

 

(Click image to enlarge)

 

The Kendall rank correlation test produced a tau of 0.55. In addition, the correlation between the two variables had a p-value of 2.2e-05. Thus, the data suggest a significant correlation between the number of Hall of Fame members that a franchise is affiliated with and the number of World Series championships a franchise has won because the observed p-value is less than the significance level set at α = 0.05.

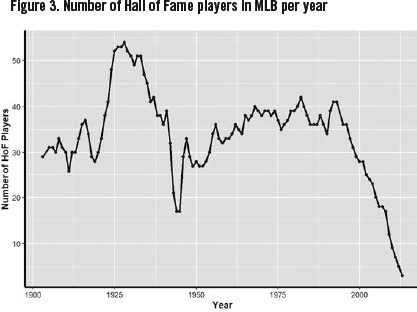
The number of Hall of Fame players present on each World Series championship team roster was then collected and plotted in Figure 2. Various points have been labeled to highlight teams that won the World Series with an outlying number of Hall of Fame players.

The number of Hall of Fame players on each World Series winning roster can be observed decreasing after the 1968 season. Therefore, a Student’s t-test was performed to determine whether the expansion of the playoffs in the 1969 season is associated with the decline in number of Hall of Fame players on the team that won the World Series. The t-test was calculated assuming the variances of both groups were equal. The results are displayed in Table 2.

 

Table 2. Number of Hall of Fame Players on Team Winning World Series Student’s T-Test Comparison

(Click image to enlarge)

 

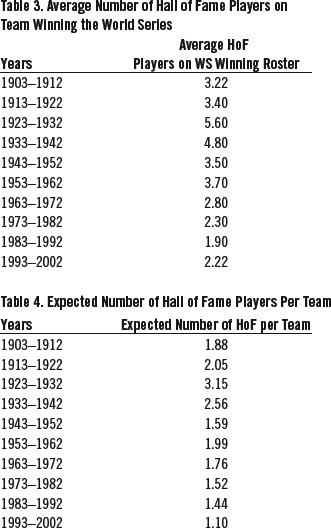
The total number of Hall of Fame players in each season from 1903 to 2013 was then counted and plotted in Figure 3. The number of players in each season was calculated by counting the number of active Hall of Fame players for a given season.

This total number of Hall of Fame players was divided by the number of teams in the American and National Leagues for each respective season in order to compute the expected number of Hall of Fame players on an MLB team.

 

(Click image to enlarge)

 

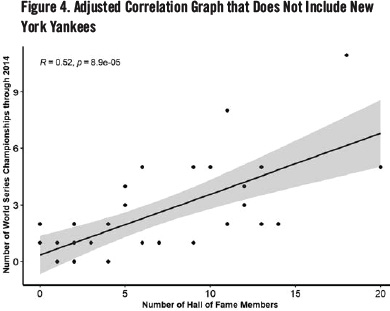
Tables 3 and 4 display the average number of Hall of Fame players on the team that won the World Series and the expected number of Hall of Fame players on each team, respectively, split into groups of ten years. Years after 2002 were omitted because players are still being elected into the Hall of Fame from the period of 2003 to present.

 

(Click image to enlarge)

 

A Chi-Square test of independence was performed between the observed number of Hall of Fame players on the World Series championship team roster and the expected number of Hall of Fame players per team for every season there was a World Series.

The Chi-Square test produced a p-value equal to 5.849e-08, which is less than the significance level of α = 0.05. This p-value indicates that the observed number of Hall of Fame players on the World Series championship team roster is significantly greater than expected.

DISCUSSION

The two goals of this project were to explore the possibility for increased rates of Hall of Fame players who have won a World Series and to attempt to explain any such elevated rates. By examining Table 1, it becomes evident that the proportion of Hall of Fame players who have won a World Series is greater than expected.

In order to explain why Hall of Fame players win the World Series more often than expected, a correlation test and graph were produced in Figure 1. This figure depicts the number of Hall of Fame members associated with a franchise and the number of World Series championships a franchise has won. A significant linear relationship can be observed from this graph. Furthermore, the New York Yankees can be observed as an outlier because of their high totals in both Hall of Famers and World Series championships.

The data in Figure 2 illustrate the number of Hall of Famers present on the roster of the team that won the Fall Classic. The 1928 and 1932 Yankees teams have the most Hall of Famers on the roster with nine each. This is unsurprising as both teams are regarded as some of the best teams in the history of baseball. Nevertheless, in seasons prior to the expansion of the playoffs in 1969, teams to win the World Series with only one Hall of Fame player were the 1919 Cincinnati Reds, 1940 Cincinnati Reds, and 1944 St. Louis Cardinals. The lack of Hall of Famers on the 1944 St. Louis Cardinals team can be attributed to ballplayers leaving MLB in response to World War II. This drastic decrease in the number of Hall of Fame players in the league during World War II is shown in Figure 3.

Interestingly, a team with zero Hall of Fame players did not occur until the 1981 Los Angeles Dodgers defeated the New York Yankees. This may be explained by 1981 being a shortened season due to the players’ strike. Moreover, it is the last time a team has come back and won the World Series after losing the first two games on the road. In addition, prior to 2000, the only other team to win the World Series without Hall of Fame players on the roster is the 1997 Florida Marlins.

The decline in number of Hall of Fame players on the World Series champion roster can be explained by a few factors. Firstly, since the 1990s, a steep decline can be observed in Figure 3 for the number of Hall of Fame players present in MLB. This decline is because fewer players who played after 1990 are eligible for induction in the National Baseball Hall of Fame. Second, the expansion of the playoffs in 1969 increased the number of rounds a team must play in order to win the World Series. Thus, the likelihood that the theoretical best team, or the team with the most Hall of Famers, wins the World Series declines—as shown by Table 2. Therefore, the expansion of the playoffs increased the odds that a team with fewer Hall of Fame players will win the World Series.

This project emphasizes that a close relationship exists between individual and team success. Talented individuals contribute to the overall winning of their team, which in turn enables players who win a World Series to be seen more favorably by the Hall of Fame voting committee. Postseason baseball has the ability to transform great players into players of legendary— Hall of Fame—status in the minds of fans and voters alike. Players like Catfish Hunter have made the Hall of Fame while players like Luis Tiant have not. Both Hunter and Tiant sport similar career statistics. However, Hunter is a five-time World Series champion and Tiant failed to win a single World Series. Likewise, one of the knocks on current great Mike Trout is the fact that “he” (his team) has failed to make a deep postseason run.

Since Hall of Famers are overly represented among World Series winners, Hall of Fame players are seen to play a demonstrably vital role in a team’s ability to win. So why then do such standouts as Ted Williams, Ty Cobb, George Sisler, and Ken Griffey Jr. all go down in history without ever winning a World Series? In the case of Ted Williams, a man who is widely regarded as the greatest hitter to ever live, the fact remains that he never won a World Series. This project sheds some light on ideas that might at first appear to be at odds. Williams’s problem certainly was not his extraordinary talent, but may have been the talent level of those around him. In his 19-year career, Williams only played six seasons during which he had more than one Hall of Fame teammate, far below the averages of World Series teams who won during his active years, as shown in Table 3.

These data support the theory that a lack of team support inhibits players such as Ted Williams from winning the World Series. The finding that the legends we often venerate as Hall of Famers are heavily influenced by the circumstances of their team’s roster should force fans (and Hall of Fame voters) to take players’ career achievements into account within the context of their teams. This will ultimately produce a more complete picture of success for individual players and teams as a whole.

One way of improving this research would be to further study the teams that have included a higher-than-average number of Hall of Fame players but failed to win a World Series. This would illustrate the importance of various factors, such as time, injuries, and team chemistry, that impact a team’s ability to win the World Series.

 

(Click image to enlarge)

 

APPENDIX

The binomial probability mass function was used to calculate the expected proportion of Hall of Fame players to win a World Series. The equation used for this calculation is:

Where x is the number of seasons not winning World Series, p is the probability of not winning the World Series, and n is the number of seasons played.

A one-tailed binomial test was calculated with a predetermined significance level of α=0.05.

A Kendall rank correlation test was chosen because the data do not come from a bivariate normal distribution. The test was also performed with the exclusion of the New York Yankees because they might be considered an influential point—as the team greatly affected the slope of the regression line and caused the coefficient of determination, R², to be bigger. The resulting p-value for the adjusted correlation test was still found to be significant at the α=0.05 level. importance of various factors, such as time, injuries, and team chemistry, that impact a team’s ability to win the World Series.

SAMUEL BORGEMENKE is a third-year undergraduate student at Ohio State University who is studying Statistics. He is from Cincinnati, Ohio, and has been a SABR member since 2019. His interest in “ringless” Hall of Famers stems from one of his favorite players, Ken Griffey Jr., who never won a World Series.

 

Notes

1. “Hall of Famers.” National Baseball Hall of Fame, 2020. https://baseballhall.org/hall-of-famers.

2. “B-R Bullpen.” BR Bullpen, 2019. https://www.baseball-reference.com/bullpen/Hall_of_Fame.

3. “BBWAA Election Rules.” National Baseball Hall of Fame, 2020. https://baseballhall.org/hall-of-famers/rules/bbwaa-rules-for-election.

4. “Best Players in MLB History to Never Win a World Series.” MLB.com, October 25, 2012. https://www.mlb.com/news/best-players-in-mlb-history-to-never-win-a-world-series/c-40041796.

5. Gough, Christina. “Most World Series Wins.” Statista, November 5, 2019. https://www.statista.com/statistics/235618/mlb–number-of-world-series-championships-by-team.

6. Baseball Almanac, Inc. “Baseball Hall of Fame Fast Facts & Frivolities.” Baseball Almanac, 2019. https://www.baseball-almanac.com/hof/hofstat.shtml.