Baseball Player Won-Lost Records: The Ultimate Baseball Statistic
This article was written by Tom Thress
This article was published in Fall 2016 Baseball Research Journal
In the Fall 2012 Baseball Research Journal, I authored an article entitled “Beyond Player Win Average: Compiling Player Won-Lost Records” in which I introduced my attempt to measure player value, Player Won-Lost records.
I calculate Player wins and losses two ways. I begin by calculating pWins, which are tied directly to team wins, by construction—the players on a team earn two pWins and one pLoss for every team win and one pWin and two pLosses for every team loss. Having constructed these, I then also construct eWins, which are neutralized for context. Statistics derived from eWins—such as eWins over Positional Average (eWOPA) and eWins over Replacement Level (eWORL)—are conceptually comparable to other sabermetric “uber-statistics,” including the various constructions of Wins above Replacement (WAR).
In this article I will explain why I believe that Player won-lost records are the best measure of player value—in essence, why Baseball Player won-lost records are the ultimate baseball statistic. The heart of this explanation is a comparison of my results to Wins above Replacement (WAR) as measured by Baseball-Reference.com and Fangraphs.
The relationship between team wins and pWins is perfect: [Actual Wins minus Actual Losses] equals [pWins minus pLosses] for any given team by construction. As such, there is not much “analysis” to be done there. But what about context-neutral wins (eWins)?
The object of analysis throughout this report will be net wins—Wins minus Losses—and/or wins above average (WOPA, in my vernacular; WAA, in the vernacular of WAR). I focus on wins relative to average for three reasons:
- First, wins above or below average are a “real” thing that can be empirically measured, whereas “replacement level” is more of a theoretical concept (although, once “replacement level” is set— at, say, .294 as is the case for Baseball-Reference and Fangraphs—it essentially becomes as empirically valid a measuring stick as .500).
- Second, for both Player won-lost records as well as for WAR, values are built up initially relative to average; comparisons to replacement level simply derive from a final step that shifts the comparison point from .500 to something else.
- Third, net wins, WOPA, and WAA are all centered on zero by construction. This simplifies the mathematics of the statistical analyses that I undertake here by eliminating the need for constant terms in any of my equations.
PLAYER WON-LOST RECORDS: eWINS VERSUS TEAM WINS
Having laid that out, we begin, then, with a basic equation that looks at the relationship between Net Wins (actual team wins minus actual team losses) and Net eWins (total eWins for the players on a team minus total eLosses for the players on a team):
Net Wins = a*(Net eWins)
This equation was fit using Ordinary Least Squares with the following results.
Table 1:
| Seasons | a | Standard Error |
R2 |
|---|---|---|---|
| 2003-15 | 2.008 | 0.049 | 0.815 |
I chose the time period investigated here, 2003 through 2015, because my source data (from Retrosheet) are generally consistent since that time at identifying the hit type (e.g., ground ball, fly ball, line drive) for all balls in play. I also investigated some longer time periods to see how consistent the results were over the longer time period. Generally speaking, the results presented here were fairly stable across earlier seasons as well.
The estimated coefficient, a, has a value of approximately two. This is, perhaps, twice what one might expect—that the coefficient in the above equation should be approximately equal to one. The reason why net eWins translate into net Team Wins at more than a one-to-one ratio is because the difference in Player winning percentage between the winning and losing team within a game tends to be fairly narrow. Specifically the pWinning percentage of players on a winning team will be 66.7 by construction (2 pWins vs. 1 pLoss). (My rationale for assigning players pLosses in team wins was explained in my earlier BRJ article). But the eWinning percentage of players on a winning team has tended to be closer to 57.6 (1.9 “wins” vs. 1.4 “losses” per game before normalization). In other words, 0.076 net eWins (0.576–0.500) translate into 0.167 net pWins (0.667–0.500), a ratio of about 2.2, which is not terribly different from the numbers in the above table.
The Standard Error of the coefficient, a, measures the uncertainty of the coefficient estimate. Given certain assumptions, we would expect the true coefficient to fall within one standard error of the point estimate approximately two-thirds of the time and we would expect the true coefficient to fall within two standard errors of the point estimate approximately 95% of the time.
The value, R2, measures the percentage of total variation in the “dependent” variable (Net Wins) that is explained by the equation—i.e., that is explained by the “explanatory” variable(s) in the equation—Net eWins, in this case. Overall, somewhat more than 80% of the variation in team wins can be explained by differences in eWins. The remaining differences can presumably be attributed to differences in the context in which player performance took place.
TEAMMATE INTERACTION
For several components of Player won-lost records, responsibility is shared between players—either between batters and baserunners or between pitchers and fielders. The values of eWins are calculated controlling for the ability of one’s teammates. For shared components, however, the team-level winning percentage is affected not only by the context-neutral winning percentages for the two sets of players sharing the components (e.g., pitchers and fielders), but also by the interaction of these two variables. This latter term is referred to by me as a “Teammate Adjustment.” If both pitchers and fielders on a team are above average at something, the team, as a whole, will be better than either its pitchers or its fielders.
To account for this interaction, then, the next equation which I investigated added teammate adjustments to the previous equation as follows.
Net Wins = a0*(Net eWins) + a1*(Teammate Adj.)
This equation was fit using Ordinary Least Squares with the following results.
Table 2:
| Seasons | a0 | Std Error | a1 | Std Error | R2 |
|---|---|---|---|---|---|
| 2003-15 | 1.956 | 0.048 | 4.170 | 0.850 | 0.826 |
The coefficient on Teammate Adjustments is approximately twice as large as the coefficient on net eWins. This is because of a difference in the nature of the two variables. Net eWins are equal to wins minus losses. So, for a record of, say, 90–72, net wins would be +18. Teammate adjustments are reported relative to .500, where 90 wins (out of 162) is only 9 games over .500 (81 out of 162 games). If the coefficient on Teammate Adjustments was constrained to be exactly equal to twice the coefficient on net eWins in the equation above, the coefficient on net eWins would be 1.961 (standard error of 0.046) and the R2 of the equation would be 0.825.
IMPACT OF BATTING vs. BASERUNNING vs. PITCHING vs. FIELDING ON TEAM WINS
Having set up a basic equation to relate eWins to Team Wins, this equation can be extended to evaluate whether the four basic factors are weighted appropriately within Player won-lost records. That is, the basic equation laid out above:
Net Wins = a0*(Net eWins) + a1*(Teammate Adj.)
can be replaced with the following equation:
Net Wins = ab*(Net Batting eWins) + ar*(Net Baserunning eWins) + ap*(Net Pitching eWins) + af*(Net Fielding eWins) + a1* (Teammate Adj.)
One might think, then, that if batting, baserunning, pitching, and fielding are weighted correctly, then the coefficients on these factors (ab, ar, ap, and af) should be equal to each other (and should all be equal to the coefficient on net eWins from the earlier equation(s), a0).
I re-arranged some terms in the basic equation outlined above to make the interpretation and analysis of the results somewhat more intuitive. Specifically, I fit the following equation (using Ordinary Least Squares):
Net Wins = a0*[(Net Batting eWins) + (1 +ar0)*(Net Baserunning eWins) + (1 + af0)*(Net Fielding eWins) + a2*(Teammate Adj.)] + a0*(1 + ap0)*(Net Pitching eWins)
This equation is mathematically identical to the previous equation, but some terms have been rearranged and coefficients have been re-presented to facilitate analysis.
- In this equation, a0 is the same as in the equation relating (Net Wins) to (Net eWins) and we would expect this coefficient to be similar in magnitude across both equations.
- The coefficient on Teammate Adjustments in the earlier equation, a1, is equal to a0*a2 in this equation. As explained above, the coefficient here, a2, has an expected value of 2.
- The coefficients, ar0 and af0, measure the difference in the weight on these two factors (ar and af) relative to the weight on the factor, batting (ab). The expected coefficients on ar0 and af0 are both zero.
- I have separated pitching from the other three factors for reasons that will become more obvious later in this article.
The final results of this equation are presented in the next table.
Table 3:
| 2003-15 | |
|---|---|
| a0 (Std. Error) |
2.064 0.078 |
| a2 (Std. Error) |
1.828 0.555 |
| ar0 (Std. Error) |
-0.275 0.264 |
| af0 (Std. Error) |
0.031 0.176 |
| ap0 (Std. Error) |
0.220 0.062 |
| R2 | 0.839 |
A few comments.
- The general coefficient, a0, is similar to earlier estimates, around 2.0.
- Batting, baserunning, and fielding seem to generally be weighted correctly. The one possible exception is baserunning, with the coefficient on ar0 being about one standard error below zero (which implies that baserunning is, perhaps, somewhat over-weighted in Player won-lost records), although a difference of one standard error is generally not viewed as statistically significant.
- The coefficient on teammate adjustments, a2, is not significantly different from two.
- Including the four factors separately improved the R2 value of the equation somewhat, from 82.6% to 83.9%.
- The coefficient on pitching, ap0, is significantly (3.5 standard errors) greater than zero. Over the most recent sample period, the coefficient on pitching here, 0.22, suggests that pitching is under-weighted in Player won-lost records by approximately 22%.
Obviously, comment 5) warrants further discussion and analysis.
One of the key findings of my work is that player wins are not additive. In fact, they are something closer to multiplicative. This is mostly because of the result noted above that the players on a winning baseball team have an average context-neutral (eWin) winning percentage of 57.6 which translates into a pWin winning percentage of 66.7. As mentioned above, this is the reason why a0 has a value of two in the equations presented so far. This multiplicative effect affects the expected impact of players who are somewhat above (or below) average. The impact of a player being slightly above average will translate into a greater impact on team wins. This effect is not taken account of in the net factor wins analyzed above. And it is this effect that explains the significant positive coefficient on ap0.
The multiplicative effect of player performance on team wins is incorporated into my calculation of eWins through an expected team win adjustment. This increases the expected player winning percentage based on the expected impact of the player’s performance on the team’s winning percentage. Expected team win adjustments are stronger for pitchers than for non-pitchers, because pitchers concentrate their performance into fewer games, so that the per-game impact of pitchers tends to be greater than the per-game impact of individual non-pitchers.
From 2003 through 2015, pitching (including pitcher fielding) accounted for 34.0% of unadjusted player decisions. But pitchers accounted for 44.3% of pWins over replacement level (excluding pitcher offense). In other words, the impact of pitchers on team wins is 30.4% greater than the impact implied by simple, unadjusted pitching decisions (44.3% / 34.0% – 1). Hence, the expected coefficient on ap0 is not zero, but is, instead, 0.304, which is not significantly different from the value of ap0 shown above.
In other words, my analysis here strongly suggests (to me) that the relative value of batting, baserunning, fielding, and pitching implied by Player won-lost records accurately reflect the relative value of these four factors on actual team wins.
SUMMARY OF RESULTS
The next table repeats the results above for my final equation and contrasts the estimated coefficients with the expected coefficients, as they were derived above (except for a0, for which the “expected” value is really an empirical question—i.e., the “right” coefficient is whatever comes out of the equation). That is, the second equation takes everything except a0 as given and only estimates a coefficient for a0.
Table 4:
| Statistical Estimates |
Expected Values |
|
|---|---|---|
| a0 (Std. Error) |
2.064 0.078 |
1.978 0.044 |
| a2 (Std. Error) |
1.828 0.555 |
2.000 — |
| ar0 (Std. Error) |
-0.275 0.264 |
0.000 — |
| af0 (Std. Error) |
0.031 0.176 |
0.000 — |
| ap0 (Std. Error) |
0.220 0.062 |
0.304 — |
| R2 | 0.839 | 0.838 |
None of the results in the first column are significantly different from the expected results in the right-hand column.
Taking all of this a step further, then, team wins over .500 can be related to eWins over positional average by the following equation:
Team Wins over .500 = a0*(eWOPA + (Teammate Adjustments))
If eWOPA (and, by extension, eWORL) is calculated correctly, we would expect the coefficient in this equation, a0, to match the coefficient of the same name in the previous equation, and we would expect the R2 here to match the R2 from that equation as well. The results are as follows.
Table 5:
| Seasons | a0 | Standard Error | R2 |
|---|---|---|---|
| 2003-15 | 1.915 | 0.045 | 0.821 |
The value of a0 perhaps changed a bit more than expected and the value of R2 is somewhat lower, but, overall, the results are reasonably similar.
WINS ABOVE REPLACEMENT (WAR) vs. ACTUAL TEAM WINS
Having looked at how the factors underlying Player won-lost records—batting, baserunning, pitching, and fielding—relate to team wins and whether, based on this analysis, these factors were correctly weighted in the calculation of Player won-lost records—specifically, wins over positional average (eWOPA, pWOPA) and replacement level (eWORL, pWORL), I next undertook a similar analysis for WAR (Wins above Replacement) as calculated and presented by Baseball-Reference.com (bWAR) as well as by Fangraphs (fWAR).
For both bWAR and fWAR, the basic calculation framework is the same. For non-pitchers (as well as for the offensive contributions of pitchers), a player’s contributions are expressed in terms of runs above average (runs below average being expressed as negative numbers) for the three non-pitching factors: batting, baserunning, and fielding. A fourth factor is then added into the mix, a positional adjustment, also expressed in runs above average (RAA). The positional adjustments are positive for “fielding-first” positions (C, SS, 2B) and negative for “offense-first” positions (1B, LF, RF; CF and 3B tend to have positional adjustments near zero). These four factors are added up to produce an aggregate RAA for the player. A final value, called Rrep by Baseball-Reference, based on playing time, is added to convert from runs above average (RAA) to runs above replacement level (RAR). RAA and RAR are then converted from runs to wins, based on the run-scoring environment in which the player played. In theory, one could apply the run-to-win converter to the individual components to create, in effect, separate values of WAA for batting, baserunning, and fielding (WAAb, WAAr, WAAf).
Pitcher WAR is somewhat more complicated but is similar in concept: a pitcher’s runs allowed are compared against average and converted into wins above average (WAAp) and replacement (WARp). BaseballReference begins with RA9—runs allowed per nine innings—and adjusts for the team’s fielding RAA; Fangraphs uses FIP—expected runs allowed per nine innings, based on strikeouts, walks, and home runs allowed. Both Baseball-Reference and Fangraphs adjust relief pitcher WAR to account for leverage. BaseballReference also calculates a unique run-to-win converter for each pitcher to reflect the impact of the pitcher on the run-scoring environment (I am not entirely sure what Fangraphs does in this regard).
Team WAR (or WAA) is then simply equal to the sum of the WAR (WAA) of the individual players on the team. In theory, I would expect the positional adjustments to balance out—every team has exactly one of every position in every inning of every game—so that, at the team level, I would expect a team’s total WAA to equal the sum of WAAb, WAAr, WAAf, and WAAp.
To test, then, whether batting, baserunning, fielding, and pitching are weighted appropriately within WAR, I fit the following equation:
Team Wins over .500 = ab*WAAb + ar*WAAr + af*WAAf + ap*WAAp
For analysis purposes, I re-arranged the terms in the above equation, as I did in my analysis of Player won-lost records earlier in this article.
Team Wins over .500 = (1 + a0)*[WAAb + (1 + ar0)*WAAr + (1 + af0)*WAAf] + (1 + a0)*(1 + ap0)*WAAp
The next two sections present and discuss my results for both bWAR and fWAR.
BASEBALL-REFERENCE: bWAR
Baseball-Reference has two pages on its website for every season which summarize position player and pitcher WAR for every team within the season.
For position players, Baseball-Reference provides data on Rbat (RAA for batting), Rbaser, Rdp (runs above average for batters at avoiding grounding into double plays—for this analysis, I combined Rdp and Rbat), Rfield, and Rpos (positional adjustments), along with total RAA (the sum of all of the aforementioned columns) and WAA, Rrep (replacement runs), RAR (RAA + Rrep), and WAR.
As I said above, in theory, I would have expected Rpos to be approximately zero at the team level. In fact, however, for the 2015 season, total Rpos across all 30 teams summed to +742 runs (+25 runs per team on average). Offsetting this, the combined total for Rbat was -700 runs. This is typical of the seasons which I examined (back to 1969). I am reasonably sure that the reason for this is that the average number of runs against which Rbat is measured excludes pitcher batting. But the sum of Rbat (and Rpos) for teams includes pitcher batting. For the 2015 NL, total Rpos was +847 vs. Rbat of -630; for the AL, total Rpos was -105 vs. Rbat of -70.
My intended analysis required that total WAA be limited to batting, baserunning, pitching and fielding, and that total WAA be equal to zero at the seasonal level, by construction. To do this, I distributed Rpos to Rbat such that the sum of Rbat across the league was exactly equal to zero—i.e., in 2015, since Rbat summed to -700, I adjusted that number up by +700; I did so proportional to the +742 Rpos—i.e., I added 94.3% (700/742) of Rpos to Rbat for every team. For Rrun, Rdp, and Rfield, I adjusted the numbers proportionally across all teams such that the sum for the season was equal to zero—e.g., in 2015, Rfield totaled +37; I therefore subtracted 1.2 runs (37/30) from each team’s Rfield value; in 2015, Rrun and Rdp both summed to zero across the league, so that no adjustments were necessary to these numbers.
On Baseball-Reference’s pitcher WAR page, they provided data for WAA, WAAadj, and WAR. The last of these was, of course, total pitcher WAR. The first two of these summed to zero at the league level in every season. I, therefore, set pitcher WAA equal to the sum of WAA and WAAadj. Based on Baseball-Reference’s explanation of its WAR for pitchers, WAAadj is an adjustment made to account for reliever leverage. As I understand it, then, at the league/team level, WAAadj ends up essentially being rounding error to re-center WAA to zero.
Having set all of that up, I fit the above equation using Baseball-Reference data from 2003–2015. The equation being solved is repeated here for reference.
Team Wins over .500 = (1 + a0)*[WAAb + (1 + ar0)*WAAr + (1 + af0)*WAAf] + (1 + a0)*(1 + ap0)*WAAp
The results in the first column of the table were estimated using Ordinary Least Squares. The results in the last column are what we would expect if the four factors—batting, baserunning, fielding, and pitching—were appropriately weighted in the calculation of bWAR.
Table 6:
| Statistical Estimates |
Expected Values |
|
|---|---|---|
| a0 (Std. Error) |
0.080 0.043 |
0 — |
| ar0 (Std. Error) |
0.085 0.328 |
0 — |
| af0 (Std. Error) |
-0.118 0.074 |
0 — |
| ap0 (Std. Error) |
0.013 0.035 |
0 — |
| R2 | 0.817 | 0.815 |
None of the coefficients are significantly different from their expected value (zero) at a 95% significance level. The value for a0 is nearly so, however (p=.064, meaning a0 differs from zero at about a 93.6% significance level (1 – p)). The value for af0 (p=.114) is also at least suggestive if, perhaps not quite “significant.”
A positive value of a0 suggests that the impact of position player WAA (i.e., batting, baserunning, and fielding) on team WAA is greater than one-to-one. In this case, a coefficient of 0.080 suggests that team wins over .500 are, on average, 8% greater than implied by team-level position-player WAA. So, for example a team with players with a combined (position-player) WAA of +12 (and 0 pitching WAA) would be expected to finish 13 games over .500 (this is the difference between a 93- and 94-win team in a 162-game schedule).
A negative value of af0 suggests that the impact of player fielding on team wins is less than the impact of batting or baserunning. In this case, a coefficient of -0.118 suggests that fielding WAA are, on average, 12% less valuable than batting or baserunning WAA in translating into team wins.
The top fielding team in MLB in 2015, according to Baseball-Reference, was the Arizona Diamondbacks at +68 Rfield. I translated that into a WAAf of 6.5. Reducing that by the 12% implied by the estimated value of af would lower that to approximately 5.7 WAA—a reduction of just under one team win (0.8). Overall, Baseball-Reference calculated a total of 6.4 WAA for the 2015 D-Backs. Reducing that by 0.8 would lower it to 5.6 WAA. The 2015 D-Backs actually finished 79–83, 2 wins below .500.
The worst fielding team in MLB in 2015, according to Baseball-Reference, was the Seattle Mariners at -68 Rfield. I translated that into a WAAf of -6.7. Reducing that by the 12% implied by the estimated value of af would lower that (in absolute value) to -5.9—a reduction of 0.8 wins. Overall, Baseball-Reference calculated a total of -7.7 WAA for the 2015 Mariners. Adjusting that by 0.8 would raise it to -6.9 WAA. The 2015 Mariners actually finished 76-86, 5 wins below .500.
CORRELATION BETWEEN PITCHING AND FIELDING
Baseball-Reference’s treatment of pitching vis-a-vis fielding makes it difficult to evaluate the accuracy of bWAR as compared to fWAR or eWOPA. This is not a criticism of Baseball-Reference’s treatment of pitching and fielding, merely a statement of fact. From the perspective of a team, Baseball-Reference begins with actual runs allowed, calculates an independent estimate of fielding runs above or below average, and attributes the difference between the two (i.e., total runs allowed minus (net) runs allowed by the team’s fielders) to the team’s pitchers. Baseball-Reference does not calculate WAR directly at the team level— WAR is constructed at the player level—and there are differences in the conversion from runs to wins for position players (where I understand the adjustment to be constant, or at least nearly-constant, across all players within a league) and pitchers (where the adjustment is calculated uniquely for each pitcher to reflect the impact of the pitcher on his own run-scoring environment). Because of these differences, it is not literally true that fielding WAA and pitching WAA can be traded off exactly one-for-one. But, it is the case, that, essentially, team-level pitching WAA and team-level fielding WAA will very nearly add up to a team-level defensive WAA based on actual runs allowed at the team level.
In other words, any “errors” in Baseball-Reference’s calculation of fielding WAA will produce nearly-exactly offsetting errors in Baseball-Reference’s calculation of pitching WAA—and vice versa. The mathematical term for this issue is Multicollinearity and this issue may affect the interpretation of the results in the above table (especially af0 and ap0). Specifically, (from the Wikipedia article on Multicollinearity), “One of the features of multicollinearity is that the standard errors of the affected coefficients tend to be large. In that case, the test of the hypothesis that the coefficient is equal to zero may lead to a failure to reject a false null hypothesis of no effect of the explanator, a type II error.” In layman’s terms, the standard errors associated with af0 and ap0 are artificially large, because of the way in which Baseball-Reference calculates bWAR.
Because of the way in which Baseball-Reference calculates fielding and pitching WAA, total WAA (or WAR), as calculated with Baseball-Reference will have virtually no “errors” on the defensive side, relative to actual runs allowed. Actual runs allowed may not track perfectly with team wins because of differences in timing (e.g., “clutch performance,” “pitching to the score”), but these differences should generally be beyond the scope of fWAA and eWOPA, as well (but not pWins and pWOPA, which explicitly measure such factors, of course). This should make bWAR a more accurate measure of actual team performance than either eWOPA or fWAR, neither of which tie their defensive measures directly to actual runs allowed at the team level.
This makes it very difficult to evaluate BaseballReference’s treatment of fielding and pitching at the player level by looking at the team-level accuracy of bWAR (or bWAA). Difficult, but not entirely impossible.
One thing worth looking at is the team-level correlation between pitching (WAA) and fielding (WAA). If there were systematic errors in Baseball-Reference’s calculation of fielding WAA, this would lead to perfectly offsetting errors in Baseball-Reference’s pitching WAA, which would lead to these two measures being negatively correlated. Hence, a negative correlation between fielding WAA and pitching WAA, at the team level, could be indicative of problems in the split between fielding and pitching.
Player won-lost records also calculate fielding and pitching measures controlling for each other. As with Baseball-Reference, a negative correlation between these two measures could indicate problems with this split.
One challenge, however, in evaluating correlations between pitching and fielding is to figure out what correlation we should expect. At one level, we might expect a correlation of zero: pitching and fielding are performed by entirely different players (outside of pitcher fielding, but (a) pitchers tend to have relatively few fielding opportunities compared to other positions, and (b) pitcher fielding is necessarily subsumed within “pitching” by Baseball-Reference, because of its decision to tie to actual runs allowed). On the other hand, good teams tend to be good at everything and bad teams—especially very bad teams—tend to be bad at everything. So, it might be reasonable to expect pitching and fielding to be positively correlated at the team level.
Fortunately for our analysis, one of the three systems being analyzed here—Fangraphs—estimates pitching and fielding independently, based on entirely independent statistics. Specifically, pitchers are evaluated based entirely on strikeouts, walks, and home runs (via FIP), while fielders are evaluated based entirely on balls in play (via UZR). The correlation between pitching WAA and fielding WAA, as measured by Fangraphs, should reflect the “true” correlation between these factors at the team level.
The next table calculates the correlation between pitching and fielding WAA for the three systems from 1969 through 2015.
Table 7
| FanGraphs | Baseball-Reference | Player W-L Records |
|---|---|---|
| 6.67% | -13.07% | 6.98% |
As measured by Fangraphs, the correlation between pitching and fielding is fairly small, but is slightly (and somewhat significantly) positive—as one might expect for the reasons suggested above. As measured by Baseball-Reference, however, the correlation between pitching and fielding is negative—not hugely, but significantly, so. This suggests to me that BaseballReference may be systematically misallocating credit for runs allowed between pitchers and fielders.
And what of Player won-lost records? The correlation between fielding and pitching as measured by Player won-lost records, 6.98%, is virtually identical to the correlation as measured by Fangraphs, 6.67%. I am very encouraged by this.
bWAR vs. ACTUAL WINS ABOVE REPLACEMENT
Both Baseball-Reference and Fangraphs use a replacement level of .294. As a final analysis, I compared bWAR to team WAR, where the latter was set equal to actual team wins minus the number of wins a .294 team would have won over that team’s total games (47.6 per 162). For this experiment, I fit the following equation:
Team Wins over .294 = a0 + (1 + apos)*WARpos + (1 + ap)*WARp
As with the previous table, the results in the first column of the table were estimated using Ordinary Least Squares. The results in the last column are what would be expected.
Table 8:
| Statistical Estimates |
Expected Values |
|
|---|---|---|
| a0 (Std. Error) |
2.152 0.847 |
0 — |
| apos (Std. Error) |
-0.092 0.033 |
0 — |
| ap (Std. Error) |
-0.039 0.036 |
0 — |
| R2 | 0.798 | 0.793 |
The coefficients, a0 and apos are both significant at a 95% confidence level (in fact, both are significant at more than a 98% confidence level).
The value of a0, 2.15, indicates that a team that amassed an actual .294 winning percentage would be expected to earn 2 WAR rather than the 0 WAR implied by a replacement level of .294.
The only sub-replacement team over the time period analyzed here was the 2003 Detroit Tigers, who went 43–119 for a .265 winning percentage, which works out to -4.3 wins over .294. Baseball-Reference shows them with +4.3 WAR.
The next two worst teams over this time period were the 2004 Arizona Diamondbacks and the 2013 Houston Astros, who both finished 51–111 (.315), 3.4 wins over .294. According to Baseball-Reference, the players on the 2004 Diamondbacks accumulated 5.7 WAR and the players on the 2013 Astros had 8.4 WAR.
The value of apos, -0.092, indicates that positionplayer WAR translate into about 9% fewer team WAR—i.e., 11 player WAR translate into only 10 team WAR. This is broadly consistent—in the sign of the coefficient if nothing else—with the earlier result suggesting that fielding WAA may be overstated by 12% or so.
The value of R2 indicates that just under 80% of the variance in team wins (over .294) can be explained by player WAR as presented at Baseball-Reference.com.
FANGRAPHS: fWAR
Fangraphs has two pages on its website for every season which summarize position player and pitcher WAR for every team within the season.
For position players, Fangraphs provides data on Batting, Base Running, and Fielding, as well as Positional values, expressed as runs above average. Fangraphs also has a column titled “League” which appears to reflect differences between the American League and National League in a particular season (e.g., in 2015, AL teams are credited with around 22 runs; NL teams are credited with around 11 runs here). Finally, Fangraphs has a column “Replacement,” which converts the previous columns (including League) from runs above average (RAA) to runs above replacement (RAR). Fangraphs then shows RAR (which is the sum of the preceding aforementioned columns) and WAR.
For a season as a whole, the sum of Fangraphs’ values for Batting, Baserunning, Fielding, Positional, and League add up to zero (or something exceptionally close to zero, most likely due to minor rounding issues). As was the case with Baseball-Reference, however, total Batting runs above average tend to be negative while Positional and League adjustments tend to be positive, on average, across all teams. To create WAA measures for Batting, Baserunning, and Fielding, all of which were centered at zero, therefore, I distributed Positional and League adjustments by team across Batting, Baserunning, and Fielding, such that the total number of Batting, Baserunning, and Fielding Runs (relative to average) were all exactly equal to zero for every season. I then converted these runs above average (RAA) measures into wins above average (WAA) measures using the ratio of WAR to RAR reported by Fangraphs.
Fangraphs’ pitcher WAR page provided team values for RA9-WAR (WAR based on actual runs allowed) and WAR (their preferred measure, based on FIP—i.e., based only on strikeouts, walks, and home runs allowed). Fangraphs did not provide any measures of either runs or wins relative to average (RAA or WAA). I converted Fangraphs’ WAR estimates (using WAR, not RA9-WAR) to WAA by simply subtracting the same number of WAR from each team such that the sum equaled zero. So, for example, in 2015, total pitcher WAR, as reported by Fangraphs was 429.8. Dividing 429.8 by the 30 MLB teams, the “replacement” portion of WAR worked out to 14.3 “wins” per team. Subtracting each team’s WAR by 14.3 produced a set of WAA measures which summed to zero across the 30 major league teams in 2015.
Having set all of that up, I fit the same equation as used earlier for eWins and bWAR, using Fangraphs data from 2003–15. The equation being solved is repeated here for reference.
Team Wins over .500 = (1 + a0)*[WAAb + (1 + ar0)*WAAr + (1 + af0)*WAAf] + (1 + a0)*(1 + ap0)*WAAp
The results in the first column of the table were estimated using Ordinary Least Squares. The results in the last column are what we would expect if the four factors—batting, baserunning, fielding, and pitching— were appropriately weighted in the calculation of fWAR.
Table 9:
| Statistical Estimates |
Expected Values |
|
|---|---|---|
| a0 (Std. Error) |
-0.043 0.043 |
0 — |
| ar0 (Std. Error) |
-0.122 0.263 |
0 — |
| af0 (Std. Error) |
-0.200 0.085 |
0 — |
| ap0 (Std. Error) |
0.190 0.051 |
0 — |
| R2 | 0.802 | 0.790 |
The coefficients on fielding, af0, and pitching, ap0, are both significantly different from their expected value (zero) at more than a 95% significance level.
A negative value of af0 suggests that the impact of player fielding on team wins is less than the impact of batting or baserunning. In this case, a coefficient of -0.200 suggests that fielding WAA are, on average, 20% less valuable than batting or baserunning WAA in translating into team wins.
The top fielding team in MLB in 2003, according to Fangraphs, was the Seattle Mariners at +78.1 Fielding Runs (above average). I translated that into a WAAf of 7.7. Reducing that by the 20% implied by the estimated value of af0 would lower that to approximately 6.1 WAA—a reduction of 1.6 wins. Overall, Fangraphs calculated a total of 47.2 WAR for the 2003 Mariners. Reducing that by 1.6 would lower it to 45.6 WAR. The 2003 Mariners actually finished 93–69, which is 45.4 wins above the .294 replacement level used by Fangraphs (and Baseball-Reference).
The worst fielding team in MLB in 2003, according to Fangraphs, was the Toronto Blue Jays at -73.5 Fielding Runs. I translated that into a WAAf of -7.2. Reducing that by the 20% implied by the estimated value of af0 would lower that (in absolute value) to -5.8—a reduction of 1.4 wins. Overall, Fangraphs calculated a total of 33.6 WAR for the 2003 Blue Jays. Increasing that by 1.4 would raise it to 35.0 WAR. The 2003 Blue Jays actually finished 86–76, 38.4 wins above the .294 replacement level used by Fangraphs.
A positive value of ap0 suggests that the impact of pitching WAR on team wins is greater than the impact of position-player WAR on team wins. In this case, a coefficient of 0.190 suggests that pitching WAA are, on average, 19% more valuable than position-player WAA in translating into team wins.
The top pitching team in MLB in 2003, according to Fangraphs, was the New York Yankees with 28.6 WAR. I translated that into a WAAp of 14.3. Increasing that by the 19% implied by the estimated value of ap0 would raise that to approximately 17.0 WAA and 31.3 WAR. Overall, Fangraphs calculated a total of 55.1 WAR for the 2003 Yankees. Increasing that by the additional 2.7 pitcher WAR derived above would raise it to 57.8 WAR. The 2003 Yankees actually finished 101–61, which is 53.6 wins above the .294 replacement level used by Fangraphs.
The worst pitching team in MLB in 2003, according to Fangraphs, was the Detroit Tigers with 2.9 WAR. I translated that into a WAAp of -11.4. Increasing that (in absolute value) by the 19% implied by the estimated value of ap0 would raise that (in absolute value) to -13.6 WAA and 0.7 WAR. Overall, Fangraphs calculated a total of 1.7 WAR for the 2003 Tigers. Decreasing that by the additional negative pitcher WAA derived above (2.2) would lower it to -0.5 WAR. The 2003 Tigers actually finished 43–119, which is 4.6 wins below the .294 replacement level used by Fangraphs (i.e, an actual WAR of -4.6).
fWAR vs. ACTUAL WINS ABOVE REPLACEMENT
Both Baseball-Reference and Fangraphs use a replacement level of .294. As a final analysis, I compared fWAR to team WAR, where the latter was set equal to actual team wins minus the number of wins a .294 team would have won over that team’s total games (47.6 per 162). For this experiment, I fit the following equation:
Team Wins over .294 = a0 + (1 + apos)*WARpos + (1 + ap)*WARp
As with the previous table, the results in the first column of the table were estimated using Ordinary Least Squares. The results in the last column are what would be expected.
Table 10:
| Statistical Estimates |
Expected Values |
|
|---|---|---|
| a0 (Std. Error) |
-0.605 0.906 |
0 — |
| apos (Std. Error) |
-0.116 0.035 |
0 — |
| ap (Std. Error) |
0.199 0.052 |
0 — |
| R2 | 0.799 | 0.788 |
The coefficients, apos and ap are both significant at a 99% confidence level.
The value of apos, -0.116, indicates that position-player WAR translate into about 12% fewer team WAR—i.e., 9 position-player WAR translate into only 8 team WAR. This is broadly consistent with the earlier result suggesting that fielding WAA is overstated by 20%. The value of ap in this equation, 0.199, is virtually identical to the value of ap0 in the previous equation. Both coefficients suggest that pitcher WAR translates into 20% more team WAR—i.e., 5 pitcher WAR translate into 6 team WAR.
The value of R2 indicates that just under 80% of the variance in team wins (over .294) can be explained by player WAR as presented at Fangraphs.com.
COMPARISON: eWOPA vs. bWAR VS. fWAR
Measuring the Accuracy of bWAA, fWAA, and eWOPA
At the team level, one would expect bWAA, fWAA, and eWOPA to correlate at least reasonably strongly with actual team wins over .500. The correlation will not be perfect (as it is for pWOPA and pWORL, by construction), of course. On offense, none of bWAA, fWAA, nor eWOPA tie to actual runs scored. And even if they did, differences in the distribution of runs scored lead to a less-than perfect correlation between runs scored (and runs allowed) and team wins. On the other hand, there is no particular reason to expect any of bWAA, fWAA, or eWOPA to do a notably better job of incorporating these differences, since none of the three are designed to capture such differences.
There are some expected differences across the three systems:
- As noted above, bWAA for pitching and fielding are constructed to tie to actual runs allowed at the team level, by construction. This might lead one to expect bWAA to correlate somewhat more strongly to actual team wins than either fWAA or eWOPA.
- Both bWAA and fWAA for relief pitchers incorporate the leverage in which relief pitchers pitched. To the extent that better relief pitchers pitch in more important situations, this should lead to a better correlation with team wins for bWAA and fWAA than for eWOPA, which does not adjust for actual pitcher leverage.
- While eWOPA are calculated based on “contextneutral” win probabilities, there are some plays—stolen bases, bunts, and intentional walks—which I do not “neutralize” for context. To the extent that these plays are incorporated within eWOPA based on their actual context, this may lead eWOPA to correlate somewhat better with actual wins than bWAA or fWAA.
But, overall, the best (only?) way to evaluate how “accurate” bWAA, fWAA, and eWOPA are, relative to one another, is to evaluate how close they come to actual wins over .500 at the team level.
Table 11 repeats results presented earlier in this article that relate actual team wins to my eWOPA (eWins over positional average) and to WAR (Wins above Replacement), as calculated by BaseballReference (bWAR) and Fangraphs (fWAR). (I evaluated WAR rather than WAA because the WAA values investigated here were at least partially constructed by me, as explained earlier in the article.)
For eWOPA, I fit the following equation:
Team Wins over .500 = a0*(eWOPA + (Teammate Adj.))
For bWAR and fWAR, I fit the following equation:
Team Wins over .294 = c + (1 + apos)*WARpos + (1 + ap)*WARp
The equations were all fit over team data from 2003 through 2015.
Table 11:
| eWOPA | bWAR | fWAR | |
|---|---|---|---|
| a0 (Std. Error) |
1.915 0.045 |
— — |
— — |
| C (Std. Error) |
— — |
2.152 0.847 |
-0.605 0.906 |
| apos (Std. Error) |
— — |
-0.092 0.033 |
-0.116 0.035 |
| ap (Std. Error) |
— — |
-0.039 0.036 |
0.199 0.052 |
| R2 | 0.821 | 0.798 | 0.799 |
In comparing the results, I would point out that the equation for eWOPA presumes that the various factors are weighted optimally (as, indeed, I showed that they are earlier in this article). For bWAR and fWAR, however, the equation corrects for any mis-weighting between position players and pitchers. As such, to the extent the results here may be biased toward one or the other, they would be biased toward the WARs.
In spite of this possible bias, the highest R2 (which measures the percentage of variance in actual team wins explained by the various equations) is for eWOPA.
There are several alternative ways to measure how “close” these measures come to actual team wins beyond the above table. Table 12 presents two such measures over two alternate time periods.
Table 12:
| bWAA | fWAA | Raw | eWOPA incl. Teammate Adj. |
|
|---|---|---|---|---|
| Correlation | ||||
| 1969-2015 | 89.7% | 88.4% | 89.9% | 90.6% |
| 2003-2015 | 89.3% | 88.8% | 90.3% | 90.8% |
| Standard Errors | ||||
| 1969-2015 | 4.931 | 5.213 | 4.926 | 4.792 |
| 2003-2015 | 5.066 | 5.118 | 4.839 | 4.726 |
The first two rows present the simple correlation between team wins over .500 and the measures being evaluated here (bWAA, fWAA, eWOPA). Correlation is a measure that ranges from -1 to 1. Numbers greater than zero indicate that teams with higher values of bWAA (for example) tend to also have more actual wins over .500 (and vice versa). A correlation of 1 (or 100%) would mean that actual wins and the measure of interest move perfectly in synch, so that 5% more bWAA would translate into exactly 5% more wins over .500.
Statisticians often refer to correlation by the letter, r. The relationship between the “r” here and the R2 in several of my earlier tables is not coincidental. In fact, for a univariate equation (i.e., y is a simple function of one variable, x), R2 is the square of the correlation coefficient, r. Not surprisingly, then, the correlation results here tell the same basic story as the R2 results told earlier: the relationships between team wins over .500 and bWAA, fWAA, and eWOPA are fairly similar, with eWOPA correlating somewhat better than bWAA and fWAA.
The last two rows calculate standard errors for bWAA, fWAA, and eWOPA. These are calculated as follows. For every team-season, the difference between team wins over .500 and the number of wins over .500 predicted by the relevant measure is calculated. For bWAA and fWAA, the “number of wins over .500 predicted” is simply equal to bWAA and fWAA, respectively. As discussed earlier, the relationship between net eWins and net team wins (and, by extension, between eWOPA and team wins over .500) is not one-to-one, but is closer to two to one. Hence, for this set of calculations, “the number of wins over .500 predicted by” eWOPA is equal to 2 times eWOPA. These differences are squared and then summed. Squaring the errors has two effects. First, a square of any number is positive, so squaring the numbers has the effect of valuing 2 the same as -2, so that positive and negative errors do not simply cancel out. Second, squaring these numbers (as opposed to simply taking the absolute value) weights larger errors more strongly than smaller errors. For example, squaring errors of 1 and 4 would produce a sum of squared errors of 17 (12 + 42) while squaring errors of 2 and 3 (which have the same simple sum: 5) would produce a sum of squared errors of only 13 (22 + 32): being off by 4 half of the time is worse than always being off by 2 or 3. The sum of squared errors is then divided by the total number of observations (1,288 team-seasons from 1969–2015) and the square root is taken. The results, then, are, essentially, average absolute errors (weighted against large errors)—so lower numbers are better.
The conclusion from the standard errors is pretty much the same as the conclusion from the correlations: eWOPA is best. Over the most recent time period (2003–15), the standard error associated with eWOPA (including teammate adjustments) is approximately 7% better than bWAA and 8% better than fWAA.
Comparing bWAA and fWAA, the results seem to clearly favor Baseball-Reference. This is as we would expect, I think, given that defensive bWAA are constructed based on actual runs scored. Given that, the fact that eWOPA is even more accurate than bWAA strikes me as truly impressive (although I’m obviously not the most objective observer of these results, of course).
COMPARISON OF FACTORS: BATTING, BASERUNNING, FIELDING, PITCHING
Proper Factor Weighting: Batting vs. Baserunning vs. Pitching vs. Fielding
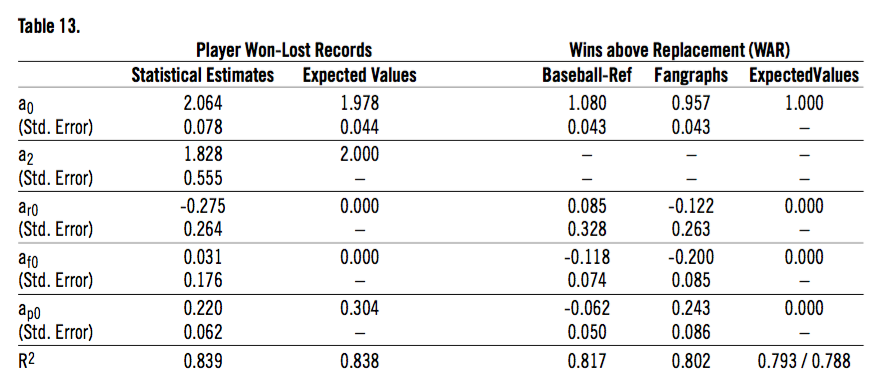
Earlier in this article, I spent a great deal of time looking at the individual factors of player value— Batting, Baserunning, Fielding, and Pitching—and assessing whether these factors were properly weighted within eWOPA, bWAA, and fWAA. Those results are repeated below.
To review, I fit the following equation for eWins, bWAA, and fWAA by factor.
Net Wins = a0*[(Net Batting eWins) + (1 + ar0)*(Net Baserunning eWins) + (1 + af0)*(Net Fielding eWins) + a2*(Teammate Adj.)] + a0*(1 + ap0)*(Net Pitching eWins)
Table 13 presents statistical results (estimated using Ordinary Least Squares) as well as expected coefficients. All three equations were estimated over data from 2003–15.
To review some key points from my earlier analysis. First, with respect to Player won-lost records:
- None of the coefficients in the equation for Player won-lost records are significantly different from their expected values.
- The impact of pitching on Player won-lost records is stronger (by 20–30 percent) than expected based on raw Player won-lost records. But this is accounted for in player eWins through adjustments for expected context and “team win adjustment”.
- The relationship between net eWins and net Team wins is approximately 2-to-1.
- The relationship between eWins and team wins is strengthened by taking explicit account of teammate adjustments, to reflect the interactive relationship between pitchers and fielders (and, to a lesser extent, between batters and baserunners).
- Overall, approximately 84% of the variance in team wins is captured within eWins.
As for the two WAR measures:
- Fielding is significantly over-weighted and pitching is significantly under-weighted within Fangraphs’ fWAR framework.
- Because of the structure of its calculations— which tie to actual runs allowed at the team level—it is difficult to evaluate the appropriateness of Baseball-Reference’s weighting of fielding and pitching. The evidence that exists, however, suggests that fielding is over-weighted by Baseball-Reference.
- Despite certain factors that should give the two WAR measures certain structural advantages vis-a-vis context-neutral eWins—relief pitcher leverage, Baseball-Reference’s use of actual runs allowed—both WAR measures explain less of the actual variance in team wins than eWins, even when optimizing the weighting of batting, baserunning, pitching, and fielding.
- As presented by Baseball-Reference and Fangraphs, less than 80% of the variance in team wins is captured within either bWAR or fWAR.
WHY ARE PLAYER WON-LOST RECORDS SUPERIOR?
The math seems very compelling to me. Player won-lost records are a better measure of actual team value—and, hence, by extension, are a better measure of player value—than WAR. Of course, I’m not the most objective observer here, but hopefully I have made a sufficiently compelling case that you agree with me.
Moving beyond the math, why are Player won-lost records superior to WAR?
The answer, I believe, is because I start from actual wins. I actually begin by calculating pWins, which tie to team wins by construction. I then pull out the context from pWins to create eWins. But starting from actual wins ensures that eWins still tie directly to team wins because eWins are still derived from actual team wins—albeit indirectly.
For example, starting from actual wins, I discovered that home runs are more valuable, relative to other hits, than conventional sabermetric wisdom believed.
Starting from actual wins, my other big discovery is that the translation from player value to team value is not linear, but is, instead, largely multiplicative. Being a little bit better than average will translate into a lot of wins. By starting from actual team wins, I was able to incorporate this finding even into my “context-neutral” wins through what I call an “expected team win adjustment.” This recognizes that a player who is somewhat above (or below) average will have a non-linear, multiplicative, impact on his team’s wins above (or below) average. The extent to which this is true will depend on how concentrated a player’s performance is within his team’s games. Because pitchers concentrate their performance more heavily than position players, this leads to pitchers having stronger expected (and actual) team win adjustments. This leads me to (correctly) weight pitcher performance more heavily than may be suggested by a simple linear analysis.
Probably the most significant difference between my eWOPA and eWORL measures versus bWAR and fWAR is in the impact of fielding on team wins. As I showed and discussed above, both WAR measures overstate the impact of fielding on team wins, by perhaps as much as 25%. In contrast, the evidence strongly suggests that my weighting of fielding is entirely appropriate. As with batting and pitching, I believe that I have gotten this weighting right because I determined the appropriate split between pitching and fielding through an objective analysis that began from a framework tied to actual team wins.
Ultimately, if you want to understand what leads to wins in Major League Baseball, you have to look at actual wins in Major League Baseball. Player won-lost records begin by looking at actual team wins, unlike WAR, which begins by looking at theoretical run values. And that is why Player won-lost records produce the best estimate of player value, either in or out of context.
TOM THRESS is an economist who lives in Chicago with his wife and two sons. He has had baseball research published in the SABR Statistical Analysis Committee’s publication “By the Numbers” and the “Baseball Research Journal.” His baseball research based on his statistic Baseball Player Won-Lost records can be found at his website baseball.tomthress.com.
References
“Baseball-Reference.com WAR Explained,” http://www.baseball-reference.com/about/war_explained.shtml.
“fWAR and rWAR,” http://www.fangraphs.com/library/war/differences-fwar-rwar.
Thress, Thomas, “Beyond Player Win Average: Compiling Player Won-Lost Records,” Baseball Research Journal, Fall, 2012.
Baseball Player Won-Lost Records, http://baseball.tomthress.com.