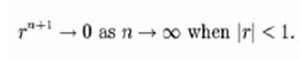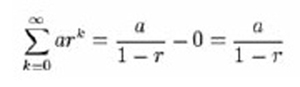The Infinitely Long MLB Plate Appearance

To those who live and breathe baseball as I do, the game was aptly described by the late A. Bartlett Giamatti in the November 1977 issue of Yale’s alumni magazine. In “The Green Fields of the Mind,” Giamatti notes, “The game breaks your heart. It is designed to break your heart. The game begins in spring, when everything else begins again, and it blossoms in the summer, filling the afternoons and evenings, and then as soon as the chill rains come, it stops and leaves you to face the fall alone.”

Not everyone has the same love for baseball, or enjoys the pitch-by-pitch nuances of the sport. Ray Fitzgerald wrote in the 1970 Boston Globe that one critic once characterized baseball as “six minutes of action crammed into two-and-one-half hours.”

I understand that baseball is not the quickest action sport. Should a person think that a major league game lasting two hours and 47 minutes—the current average—is a long time, then they might run screaming from the idea of an infinitely long plate appearance. Such an event is, of course, thoroughly unlikely, but it could happen.

A standard baseball plate appearance, with its strategic mix of balls, strikes, and foul balls can, mathematically, take an infinitely long time to complete … in fact, four times infinitely long to complete, which is just infinitely long.

For our purposes, we will define a plate appearance as PA = H + BB + K + HBP + SH + SF + DI + E+ DFO where:

• PA = Plate Appearance
• H = Hit (single, double, triple, or home run)
• BB = Walk (Four balls before three strikes)
• K = Strikeout (Three strikes before four balls)
• HBP = Hit by Pitch
• SH = Sacrifice Hit
• SF = Sacrifice Fly
• DI = Defensive Interference
• E = Batter reaches base due to a defensive fielding error
• DFO = Defensive Fielding Out – fly out, foul out, or ground out

An official plate appearance is completed when the batter reaches base via a hit, walk, strikeout, is hit with a pitch, sacrifices to attempt to advance a runner, reaches on Defensive Interference, reaches on a defensive fielding error, or is retired by a defensive fielding out.

The reason these calculations are monumental is because one cannot derive the probability of walks or strikeouts based on the pitches you have seen, because in one calculation equation there are multiple unknowns, giving an infinite number of solutions. My calculations allow a person to calculate the expected probability of a ball, a strike, and a foul, which in turn could yield the true probability of a resulting batting line of walks, strikeouts, and the pitch put in play results that a player actually achieved.

As you will see, 57 ways exist to walk and 84 ways to strike out; this also includes an infinite number of pitches thrown in some instances. This is easily proven by using an infinite geometric series.

INFINITE GEOMETRIC SERIES

An infinite geometric series is an infinite series whose successive terms have a common ratio. Such a series converges if (and only if) the absolute value of the common ratio is less than one (| r | < 1). Its value can then be computed from the finite sum formula

Since:

Then:

(Click images to enlarge.)

 

Any pitch put in play, or that does not end with a walk or strikeout, automatically ends the plate appearance. Non-hit balls that do not end a plate appearance (and are not inclusive of a walk or strikeout) are classified into four categories:

• B – Ball
• S – Swinging Strike, Called Strike, or Foul Ball
• F – Strike – Foul Ball
• K – Strike – Called Strike or Swinging Strike… where P(B), P(S), P(F), and P(K) are all between [0,1] and sum to 1 inclusive of those Put in Play (PIP), i.e. P(B)+P(S)+P(PIP)=1. P(S) = P(F)+P(K)

An infinitely long at bat, for example, is the 57th described way that a batter can walk.

• Batter Pitch 1 – S, Strike
• Batter Pitch 2 – S, Strike
• Batter Pitch 3 – F, Fouls a ball to infinity
• Batter Pitch 4 – B, Ball
• Batter Pitch 5 – F, Fouls a ball to infinity
• Batter Pitch 6 – B, Ball
• Batter Pitch 7 – F, Fouls a ball to infinity
• Batter Pitch 8 – B, Ball
• Batter Pitch 9 – F, Fouls a ball to infinity
• Batter Pitch 10 – B, Ball Four – Plate Appearance completed resulting in a BB.

All 57 combinations that result in a walk are detailed in this PDF file.

And all 84 combinations of events resulting in a strikeout are detailed in this PDF file.

Here is an example in which a batter will see pitches which result in a walk or strikeout but does not complete his at-bat with a pitch in play (PIP):

Ball – B	0.4000	P(B)
Strike – S	0.6000	P(S)
Foul – F	0.2400	P(F)
Str-NonF – K	0.3600	P(K)=P(S)-P(F)
TotBBK – T	1.0000	P(PA)=P(B)+P(F)+P(T)
TotPIP – P	0.0000	P(PIP)=1-P(B)-P(S)

Results using the preceding combinations of events yield

• Prob (Walk) – 25.303%
• Prob (Strikeout) – 74.687%
• Prob (PIP Plate App) – 00.000%

 

A more realistic example is of a more typical MLB player. Said player walks 8.86% of the time, strikes out 18.87% of the time, and puts a ball in play 72.27%. Although we know how many walks and strikeouts a player experiences based on the amount of pitches seen, the actual pitches do not accurately translate into the real world results of the exact P(B), P(K), P(F), or P(PIP). This formula allows you to reverse-calculate how many balls, strikes, foul balls, and PIP balls that a batter SHOULD have seen throughout his season to recreate his final walk, strikeout, and PIP results.

Ball – B	0.3611	P(B)
Strike – S	0.4167	P(S)
Foul – F	0.1667	P(F)
Str-NonF – K	0.2500	P(K)=P(S)-P(F)
TotBBK – T	0.7778	P(PA)=P(B)+P(F)+P(T)
TotPIP – P	0.2222	P(PIP)=1-P(B)-P(S)

Results using the preceding combinations of events yield

• Prob (Walk) – 8.859%
• Prob (Strikeout) – 18.866%
• Prob (PIP Plate App) – 72.274%

 

So although a game may seem to be slow, with each inning or plate appearance seeming to take forever, be thankful that it does not actually take forever … even though it could—four times over!

Play Ball!

BRIAN YONUSHONIS was born and raised in DuBois, Pennsylvania. He manages a large software testing team in the casino gaming industry and enjoys the pure mathematics of his work. He always encourages his staff to work hard and stay sharp by educating them- selves anytime they get the chance and keeps them moving forward in the face of tough economic times. As Satchel Paige said, “Ain’t no man can avoid being born average, but there ain’t no man got to be common.”