The Possible Effect of Steroids on Home-Run Production

In a recent paper entitled “On the Potential of a Chemical Bonds: Possible Effects of Steroids on Home Run Production in Baseball,”1 physicist Roger Tobin develops a systematic analysis showing how performance-enhancing drugs (PEDs) taken by an already highly skilled player could produce a dramatic increase in home-run production. Tobin starts by looking statistically at home-run production during the “steroid era” (1994—2003) compared to earlier eras. The number of home runs hit by a player is the product of balls in play and home runs per balls in play (HRBiP). Tobin argues that the former involves skills and strategies that are not likely affected by PEDs. He, therefore, takes HRBiP as his metric for comparing home-run production in different eras. In figure 2 of his paper, he shows that, for elite home-run hitters in the pre-steroid era (Aaron, Ruth, Mays, Killebrew, Robinson), HRBiP was approximately 0.10, whereas for hitters in the steroid era (Bonds, Sosa, McGwire, Griffey, Palmeiro) the number jumped to 0.15, a 50 percent increase.

Tobin then investigates whether it is plausible that such a large increase can be attributed to PEDs. In section 2, entitled “What Do Steroids Do?” he presents lots of evidence from the scientific literature justifying his starting assumption for the remainder of the analysis. Namely, he assumes that the main effect of steroids vis-à-vis home-run production is to increase the batter’s muscle mass by 10 percent. Since I have no expertise in this area, I will simply take it as a reasonable starting point. Tobin next develops section 3, entitled “How Much Can More Muscle Enhance Home- Run Production?” This section is really the heart of the paper and the one I will discuss at length. Tobin’s chain of reasoning involves two distinct steps:

1. Increased muscle mass results in higher bat speed and therefore higher batted-ball speed;
2. Higher batted-ball speed results in longer fly balls and therefore higher

Step 1 involves partly biomechanics and partly physics. Step 2 involves partly physics and partly statistics. Tobin arrives at the following conclusion: It is plausible that a 10 percent increase in muscle mass can lead to a 50 percent increase in HRBiP for the elite home run hitters.

In the present paper, I will discuss the steps in the analysis chain, first presenting Tobin’s argument and then my own. Although Tobin and I may disagree on some details, I will end up agreeing with his essential conclusion.

MUSCLE MASS AND BATTED-BALL SPEED

Tobin initially argues that a 10 percent increase in muscle mass leads to the batter supplying a 10 percent greater force to the bat, resulting in a 5 percent increase in bat speed. The argument is essentially one of energy conservation, where the work done by the batter in applying a force to the bat over a fixed distance is converted to kinetic energy of the bat. Since kinetic energy is proportional to the square of the velocity, a 10 percent greater force leads to a 5 percent increase in bat speed. In a “Note added in proof,” Tobin revises his estimate downward to 3.8 percent, based on Robert K. Adair’s argument that the work provided by the muscles is converted to kinetic energy that is shared between the bat and some fraction of the body mass of the batter, mainly the arms.2 The essential point is that both the bat and the batter’s arms are moving. Therefore not all of the work provided by the body muscles goes into kinetic energy in the bat, and a fraction must also go into kinetic energy of the body. In an unpublished article that I have posted on my website,3 I have estimated that only about half the kinetic energy goes into the bat. With the additional assumption that half of the batter’s pre- steroid weight is muscle, Tobin and I both agree that a 10 percent increase in muscle mass can lead to about a 3.8 percent increase in bat speed.

From a purely physics point of view, the easiest part of the analysis is to estimate how an increase in swing speed affects batted-ball speed. Suppose a pitched ball crosses the plate at 85 mph, a reasonable value for a good fastball given that the ball loses about 10 percent of its speed between pitcher and batter. Suppose also that the pre-steroid batter swings the bat at 70 mph at the sweet-spot location. Then, if we assume a perfect head-on collision, the resulting batted ball will exit the bat at about 100 mph. If such a ball is slightly undercut, giving it backspin, and is launched at an angle of 30 to 35 degrees, it will travel close to 400 feet. Suppose now the post-steroid batter swings the bat 3.8 percent faster, or 72.7 mph. Then the batted-ball speed will increase to about 103 mph,4 a 3 percent increase and a number Tobin agrees with in his “Note added in proof.”

So, Tobin and I both conclude that a 10 percent increase in muscle mass can result in a 3 percent increase in batted-ball speed, a number that is on very solid footing. We next examine how such an increase will affect home-run production.

BATTED-BALL SPEED AND HOME-RUN PRODUCTION

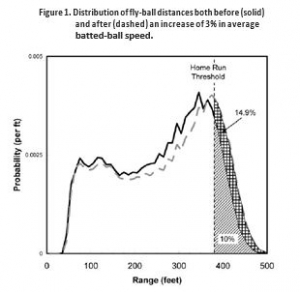
To estimate how a 3 percent increase in batted- ball speed affects home-run production, an aerodynamics model is needed to determine the additional distance traveled by a fly ball. When we use statistical information on the distribution of fly-ball distances relative to the fence, we can estimate the change in HRBiP. Unfortunately, that statistical information is not readily available, so Tobin resorts to a numerical simulation. For a given aerodynamics model,5 he assumes a normal distribution of batted-ball speeds and launch angles to calculate a distribution of fly-ball distances. He defines a home run to be a fly ball that has a height of at least 9 feet at a distance of 380 feet from home plate. He then adjusts the parameters of the normal distributions until the distribution results in 0.10 HRBiP, the baseline number for elite batters. The resulting fly-ball distribution is shown as the solid curve in figure 1. He then repeats the calculation with the mean batted-ball speed increased by 3 percent, as expected for a 10 percent increase in muscle mass, resulting in the distribution shown by the dashed curve in the figure. He finds HRBiP increase to 0.149, an increase of nearly 50 percent. 

Given the importance of figure 1 for the conclusion of the analysis, it is worthwhile discussing it in more detail. The figure shows that the distribution of fly-ball distances is smooth and continuous, whereas a home run is a binary event on the tail of that distribution. For elite home-run hitters, the slope of the distribution at the home-run threshold (380 feet) must be very steep to achieve simultaneously the 10 percent HRBiP figure and the known rarity of very long home runs— say, those in the vicinity of 500 feet or greater. The steepness of the slope means that there must be a lot of near misses, so that a small change in the mean of the fly-ball distribution can have a large effect on the fraction falling above the home-run threshold.

There is an alternate way of reaching the same conclusion, using data compiled on actual home-run distances for the 2007 MLB season.6 By inspecting the distance of the landing point from the nearest fence, one can estimate that each additional foot of fly- ball distance increases the home-run probability by

4 percent. Combining that with the aerodynamics “rule of thumb” that each additional mph of batted- ball speed increases the fly-ball distance by 5.5 feet, along with the previously estimated mean increase of 3 mph in batted-ball speed, and one arrives at a 66 percent increase in home-run probability, a number even larger than Tobin’s estimate. Adair has conducted a similar analysis. Based on his detailed study of home- run statistics, he estimates that each additional percent of fly-ball distance increases home-run probability by about 7 percent.7 If we use 380 feet as the baseline home-run distance, a 3 mph increase in batted-ball speed leads to a 4.3 percent increase in batted-ball distance and therefore a 30 percent increase in home-run probability. Putting together all these independent analyses, I find that an increase in HRBiP in the range of 30—70 percent is completely plausible.

SUMMARY AND CONCLUSIONS

I find that the conclusion reached by Tobin, that a 10 percent increase in muscle mass can lead to a large increase in home-run probability, is well supported by my own analysis. In fact, Tobin puts the increase in the range 30—70percent, depending on the details of the underlying assumptions. Obtaining a precise number is not really the point of the paper, but rather that a modest increase in muscle mass can lead to a very large increase in HRBiP. On that, we both agree.

ALAN NATHAN, professor of physics at the University of Illinois since 1977 and a fellow of the American Physical Society, is the author of more than 80 publications in scientific journals. His research specialty is experimental nuclear/particle physics. He has written numerous papers on the physics of baseball, primarily on the physics of ball–bat collision and on baseball aerodynamics. His website devoted to the physics of baseball is www.npl.uiuc.edu/~a-nathan/pob.

 

Acknowledgments

I thank Professor Roger Tobin for many interesting discussions, for a critical reading of this paper, and for providing the figure, and Greg Rybarczyk for providing the 2007 home-run data. And I thank my mentor, Professor Bob Adair, for his seminal contributions to our understanding of the science of baseball.

 

Notes

1. The paper is published in American Journal of Physics 76 (2008): 15—20. A copy can be downloaded for personal use at http://webusers.npl.illinois.edu/~a-nathan/pob/Tobin_AJP_Jan08.pdf.

2. The argument is presented in Adair’s book The Physics of Baseball, 3d (New York: HarperCollins, 2002). See the discussion in chap. 6, “The Optimum Bat Weight”. Note particularly figure 6.1 (page 117) and the formula on page 139.

3. See http://webusers.npl.uiuc.edu/~a-nathan/pob/swingspeedmass.pdf.

4. In Tobin’s paper, the factors multiplying vbat and vpitch in equation 1 are approximately 2 and 0.2, respectively.

5. Tobin recognizes that there is uncertainty in the so-called drag and lift coefficients that are needed to carry out the trajectory However, the uncertainty does not alter his principal conclusion.

6. See hittrackeronline.com.

7. Adair, 97