Do Clutch Hitters Exist?
This article was written by Dick Cramer
This article was published in 1977 Baseball Research Journal
 The idea that there are batters whose hits are more noteworthy for their timeliness than for their quality is probably as old as the game itself. Efforts to measure “clutch-hitting” systematically include the RBI, one of the three most universal batting statistics, and more recently, the “game-winning hit”. It is my own belief that clutch hitters, even if a few perhaps exist, have a negligible effect on the outcome of a pennant race.
The idea that there are batters whose hits are more noteworthy for their timeliness than for their quality is probably as old as the game itself. Efforts to measure “clutch-hitting” systematically include the RBI, one of the three most universal batting statistics, and more recently, the “game-winning hit”. It is my own belief that clutch hitters, even if a few perhaps exist, have a negligible effect on the outcome of a pennant race.
The question of whether or not clutch hitters exist should be a fundamental issue in Statistical Analysis. Pete Palmer and I believe that one can explain most of the final season standings as some properly formulated total of the individual players’ records. For example, the BRA considers only total bases, walks, hits, and so forth, without reference to the game situation when these occurred. Certainly a home run which occurs late in a tie game is more valuable to a team than one which occurs in a one-sided game. But Pete and I have always suspected that it is a matter of luck, not “clutch-hitting”, if a particular player gets more than his share of dramatic hits. Should there however be evidence that we are wrong, then statistical analyses must somehow be revised to reflect the timeliness as well as the quantity of hitting.
In order to determine whether clutch hitters exist, we need a measure of hitting timeliness and a measure of hitting quantity. The inadequacies of the RBI and the “game-winning hit” as measures of timeliness have been deplored by many authorities. However, the brothers E.G. and H.D. Mills devised a very clever and irrefutable measure.[fn]E.G. Mills and H.D. Mills, “Player Win Averages” (A.S. Barnes: Cranbury, N.J., 1970) describes the method and their 1969 results. Pete Palmer supplied me with their 1970 season results. To our knowledge, no further results exist.[/fn] The probable outcome of a baseball game was determined by computer play for every one of the almost 8000 possible situations (two out, none on, score tied, top of 2nd; runners at 2nd and 3rd, bottom of 6th, home team trailing by two; etc.) at the average level of hitting for a particular season. Then each participant in every play in every game of the season is given a certain number of “Win” or “Loss” points, according to how much his involvement in the play advances or reduces his team’s chance of winning the game.
For example, a solo home run in the ninth inning of a game in which one team is leading by six runs is worth only about 5 “Win” points; but Bobby Thomson’s home run (in a very important game) increased the Giants’ chances of victory from 25% to 100% and was worth 1470 “Win” points. A player’s “Win” and “Loss” points are accumulated over a season to yield his “Player Win Average”. PWA’s for 1969 varied from Versalles’ .330 to McCovey’s .677 and for 1970 from Doyle’s .374 to McCovey’s .648. Of course hitting a Thomson-timely home run in any game has a substantial effect on a player’s whole season’s PWA, increasing it by 40 points even for an everyday player.
The Player Win Average is without doubt a perfect measure of which hitters (and pitchers) are winning and losing games. But its computation, with the requirement of an accounting for every situation in every game, is forbiddingly expensive even when the data are available, and quite impossible in general since play-by-play information is not saved by the major leagues.
As a measure of the quantity of hitting for players in 1969 and 1970, I will use the Batter Win Average (BWA), a further refinement of the BRA concept discussed in the 1974 Baseball Research Journal. The BWA and BRA depend on a fundamental empirical relationship in baseball play; the number of runs scored in league play is nearly equal to the product of league plate appearances, league slugging percentage, and league on-base average, provided that the on-base average takes appropriate account of reached on errors and grounded into double plays:
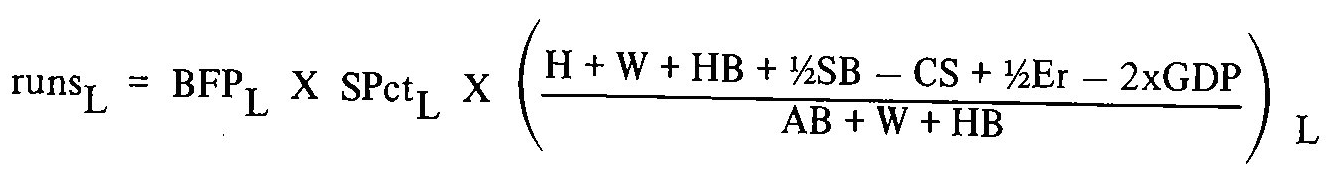
(where the subscript L refers to league totals and applies to the individual items in the on-base average)
Therefore for any individual player one can also use the above equation to compute the number of runs the league would have scored if the player had been replaced in all his plate appearances by an average hitter. The difference in the two league run totals, + or -, reflects the batter’s above- or below-average skills in producing runs for his team. A further correction is needed for “indirect runs”-runs resulting from extra plate appearances contributed or denied to his team by a player’s higher- or lower-than-average on-base average. The total + or – “offensive run production” (OffR) of a batter is divided by his plate appearances and a normalizing factor reflecting the level of hitting in that season to yield his BWA. The validity of this whole procedure is shown from its improved ability to account for team run-scoring and victories.
To make these new statistics somewhat tangible, the following table showing the highest and lowest BWA players in each league in 1969 and 1970 is given:
| Season | Player | B.A. | HR | BRA* | BFP | RC** | OffR | BWA |
|---|---|---|---|---|---|---|---|---|
| 1969 | McCovey | .320 | 45 | .277 | 623 | 172 | +76.0 | +.130 |
| 1970 | McCovey | .289 | 39 | .248 | 638 | 158 | +63.7 | +.099 |
| 1969 | Killebrew | .276 | 49 | .244 | 709 | 173 | +73.1 | +.109 |
| 1970 | Yastrzemski | .329 | 40 | .247 | 697 | 172 | +73.5 | +.110 |
| 1969 | Garrido | .220 | 0 | .048 | 251 | 12 | -16.4 | -.071 |
| 1970 | Lanier | .231 | 2 | .049 | 463 | 23 | -36.7 | -.079 |
| 1969 | Cullen | .209 | 1 | .039 | 277 | 11 | -21.6 | -.086 |
| 1970 | Thompson | .219 | 0 | .049 | 318 | 16 | -22.1 | -.074 |
* BRA computed with a -2xGDP term in the numerator of the OBA. But the ½Er term is excluded, as no individual player totals exist.
** Runs Contributed (RC) = BRAXBFP. Indicates the runs the batter would contribute to a lineup of equally skilled batters, not the runs he would contribute to a typical lineup.
The BWA is tedious to compute with a slide rule or ordinary calculator but is almost as accessible as a batting average with a programmable calculator such as the Hewlett-Packard HP-65.
To summarize the discussion so far, both the PWA and the BWA are measures of overall batting skill. The PWA is a pure measure of clutch hitting. As its inventors say: “We have made the when the dominant factor, with no regard for the kind of what that happened.” The BWA is a pure measure of hitting quantity. Whether a particular home run is meaningless or Thomson-timely, it will still raise the everyday player’s BWA by an identical three points. Thus a comparison of the PWA’s and BWA’s of players in the 1969 and 1970 seasons should provide considerable insight into the importance of clutch hitting.
My first comparison was to confirm a study by Pete Palmer, who had found that PWA’s and BWA’s are highly correlated. In fact, if one knows a player’s BWA, one can predict his PWA with high accuracy using the following equation:
PWA = (BWA) x (1.37) + .484
This means that most — about 80% — of the differences among player’s PWA’s are really attributable to differences in the quantity of their hits, not to differences in the timeliness of their hits. For example, McCovey had the highest NL PWA’s in both 1969 and 1970 because, as his highest BWA’s indicate, his chances of hitting a home run were unusually high in any situation, important or not, and because his chances of making an out and thereby reducing the Giant’s chances of winning were unusually low, clutch situation or not.
However, there were numerous players in 1969 and 1970 who had much higher or lower PWA’s than would be predicted using their BWA and the above equation. These deviations from prediction, known technically as residuals, vary from +.067 for Carlos May’s 1969 season to -.068 for Fuentes’ 1970 season. If one believes in clutch and non-clutch players, the clutch players must be the May’s, the ones with higher than predicted PWA’s, and the non-clutch players must be the Fuentes’, the ones with lower than predicted PWA’s. If one does not believe in clutch players, then Carlos May was lucky (along with the White Sox) in 1969 in the timeliness of his hits, and Fuentes was unlucky in 1970. And essentially our central problem “Do clutch hitters exist?” becomes one of “How can you distinguish between skill and luck?”
Statisticians (the professionals) have devised several ways to decide whether such a set of-differences is “significant” — in this case, caused by skill — or “insignificant” — caused by luck. Often one can place an outside limit on the differences that might reasonably be attributed to luck; if the differences are larger than this limit, then there must be other factors involved. In our problem such a limit cannot be rigorously established. Recalling however, that a single Thomson-timely home run will raise a season PWA by +.040, it is my opinion that the
observed residuals for 350 player-seasons can scarcely be much larger than what might be expected to result from luck. Furthermore, the overall distribution of residuals is “normal”, that is, in a fashion far more consistent with luck than with a pattern in which a few players hit in especially timely fashion.
There remains one more test which is particularly clear-cut and easy to understand. If clutch hitters really exist, one would certainly expect that a batter who was a clutch hitter in 1969 would tend also to be a clutch hitter in 1970. But if no such tendency exists, then “clutch hitting” must surely be a matter of luck. After all, the only means of ever identifying a clutch hitter would be by his consistency, if not from situation to situation at least from season to season.
Such a test is easily performed, by trying to correlate the residuals for players in 1969 with residuals for the same players in 1970. Not even a hint of such a correlation exists (r2 for 60 National League players was .038 and for 62 American League players was .055). This means that there is no tendency for players who were clutch hitters in 1969 to be clutch hitters in 1970. True, a few of the “clutch hitters” in 1969 were also “clutch hitters” in 1970; but as many became “unclutch” and most became average, exactly as would be expected if “clutch hitting” is really a matter of luck.
Although I have established clearly that clutch-hitting cannot be an important or a general phenomenon, a stubborn believer might still ask about the few players who appeared to be “clutch hitters” in both 1969 and 1970. As a challenge for such diehards, I present a scrambled list of the most consistent “clutch” and the most consistent “unclutch” hitters in 1969 and 1970. (To be considered, a player had to have more than 400 BFP’s and be either “clutch” or unclutch” in both 1969 and 1970.) Remembering that sheer guesswork will make you about half right, can you unscramble the list?
1. Yastrzemski 5. Andrews 9. Blair
2. Cleon Jones 6. T. Davis 10. Rader
3. Sanguillen 7. Freehan 11. Javier
4. Kaline 8. Billy Williams 12. Alex Johnson
To give away the first answer in advance, Yaz was the most consistently untimely hitter in the majors in 1969 and 1970. But no one who saw Yastrzemski play in September 1967 would ever believe that “Carl is a good hitter, but not quite as strong when a game or the pennant is on the line”! The full answer to the quiz above is that the odd-numbered batters are the untimely hitters and the even-numbered batters are the timely hitters.
Good hitters are good hitters and weak hitters are weak hitters regardless of the game situation. But there is no reason why a weak hitter shouldn’t be fortunate enough to get a series of fat pitches or good swings in crucial situations. Given enough time, this might even happen over some player’s whole career. Maybe luck was the basis of the reputation of a Henrich or a Reese as a clutch hitter-but let me hasten to add that Henrich and Reese were certainly exceptionally good hitters simply on the basis of the quantity of their hits, as well as, perhaps, the timeliness of their hits.
So fades a legend — but after all, what was really meant when someone was called a “clutch hitter”? Was he really a batter who didn’t fold under pressure-or was he a lazy batter who bothered to try his hardest only when the game was on the line?
DICK CRAMER has been doing sabermetrics for just about as long as anyone alive. He started analyzing baseball statistics in the middle 1960s, not long after graduating from Harvard, and by 1969 Cramer had discovered (or re-invented) a worthy metric now known as OPS. In 1971, Cramer discovered SABR via a squib in “The Sporting News”; in short order, Bob Davids introduced him to Pete Palmer. In the ‘70s, Cramer served SABR in various positions and published a great deal of research, including work on clutch hitting that remains a touchstone well into the 21st century. In 1980, Cramer co-founded STATS Inc. and remained involved with that company until 1994. After a decade-long hiatus, Cramer returned to baseball in 2004, doing important work with Dave Smith and Retrosheet since then. He was honored with SABR’s Henry Chadwick Award in 2015.


